What Is The Decimal For 2 1/2
bemquerermulher
Dec 05, 2025 · 8 min read
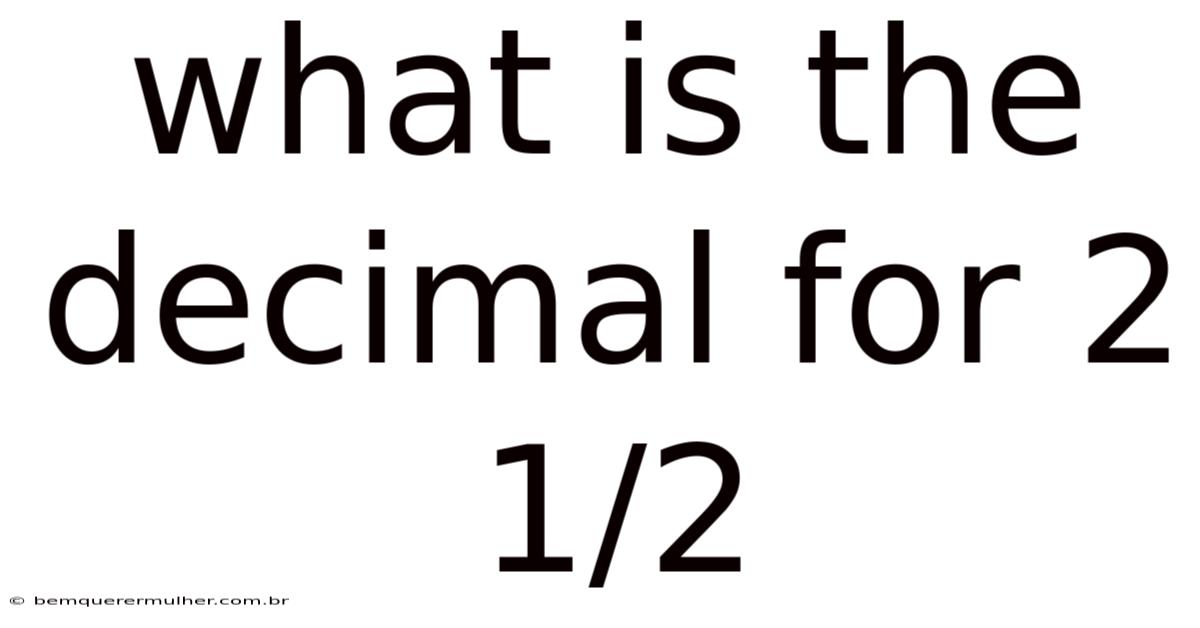
Table of Contents
Converting the mixed number 2 1/2 to a decimal involves understanding the place value system and how fractions fit into it. This article provides a comprehensive guide on how to convert mixed numbers to decimals, focusing specifically on 2 1/2, and also explores related concepts to deepen your understanding.
Introduction
Converting fractions and mixed numbers to decimals is a fundamental skill in mathematics, essential for various applications in daily life, from cooking to engineering. A mixed number, such as 2 1/2, combines a whole number and a fraction. To convert it to a decimal, we need to express the fractional part as a decimal and then add it to the whole number. This article will guide you through a step-by-step process, ensuring you understand not just the "how" but also the "why" behind the conversion.
Understanding Mixed Numbers
Before diving into the conversion, let's clarify what a mixed number is. A mixed number consists of two parts:
- Whole Number: The integer part of the number.
- Fraction: A fraction less than one, representing a part of a whole.
In the mixed number 2 1/2:
- 2 is the whole number.
- 1/2 is the fraction.
Understanding this separation is crucial because we treat each part differently during the conversion process.
Steps to Convert 2 1/2 to Decimal
Here are the steps to convert the mixed number 2 1/2 to a decimal:
- Identify the Whole Number: The whole number in 2 1/2 is 2. This part will remain as is and will be the integer part of our decimal.
- Convert the Fraction to a Decimal: To convert the fraction 1/2 to a decimal, divide the numerator (1) by the denominator (2).
- Perform the Division:
- 1 ÷ 2 = 0.5
- Combine the Whole Number and Decimal: Add the whole number to the decimal obtained from the fraction.
- 2 + 0.5 = 2.5
Therefore, the decimal representation of 2 1/2 is 2.5.
Step-by-Step Breakdown
Let's break down each step in detail to ensure clarity.
Identifying the Whole Number
The whole number part of the mixed number is straightforward. In 2 1/2, the whole number is 2. This number represents two complete units and will be the integer part of the decimal we are trying to find.
Converting the Fraction to a Decimal
The key to converting a fraction to a decimal is division. The fraction 1/2 means "1 divided by 2." This division gives us the decimal equivalent of the fraction.
Performing the Division
To divide 1 by 2:
- Since 1 is smaller than 2, we add a decimal point and a zero to 1, making it 1.0.
- Now, divide 10 by 2. 2 goes into 10 five times (2 × 5 = 10).
- So, 1 ÷ 2 = 0.5
Thus, the decimal equivalent of the fraction 1/2 is 0.5.
Combining the Whole Number and Decimal
Once we have the decimal equivalent of the fraction, we add it to the whole number.
- Whole number: 2
- Decimal equivalent of 1/2: 0.5
- Adding them together: 2 + 0.5 = 2.5
Therefore, 2 1/2 as a decimal is 2.5.
Alternative Method: Converting to an Improper Fraction
Another method to convert a mixed number to a decimal involves first converting it to an improper fraction.
- Convert the Mixed Number to an Improper Fraction:
- Multiply the whole number by the denominator of the fraction: 2 × 2 = 4.
- Add the numerator to the result: 4 + 1 = 5.
- Place the result over the original denominator: 5/2.
- Divide the Numerator by the Denominator:
- Divide 5 by 2: 5 ÷ 2 = 2.5
This method also results in 2.5 as the decimal representation of 2 1/2.
Understanding the Decimal System
To fully appreciate the conversion, it's important to understand the decimal system. The decimal system is a base-10 number system, meaning each position in a number represents a power of 10.
- Whole Numbers: To the left of the decimal point, we have the ones place (10⁰), the tens place (10¹), the hundreds place (10²), and so on.
- Decimals: To the right of the decimal point, we have the tenths place (10⁻¹), the hundredths place (10⁻²), the thousandths place (10⁻³), and so on.
In the decimal 2.5:
- 2 is in the ones place.
- 5 is in the tenths place.
This means 2.5 is 2 ones and 5 tenths, which is the same as 2 + 5/10. Simplifying 5/10 gives us 1/2, so 2.5 is equivalent to 2 1/2.
Common Fractions and Their Decimal Equivalents
Knowing common fraction-to-decimal conversions can save time and effort. Here are a few examples:
- 1/4 = 0.25
- 1/2 = 0.5
- 3/4 = 0.75
- 1/5 = 0.2
- 2/5 = 0.4
- 3/5 = 0.6
- 4/5 = 0.8
Memorizing these conversions can make working with fractions and decimals much easier.
Practical Applications
Converting mixed numbers to decimals is not just a theoretical exercise; it has many practical applications.
- Cooking: Recipes often use fractions, but measuring tools are sometimes calibrated in decimals.
- Construction: Measurements in construction often involve fractions of inches, which need to be converted to decimals for precise cuts.
- Finance: Calculating interest rates or dividing costs can involve converting fractions to decimals for accuracy.
- Science: Scientific measurements often require converting fractions to decimals for calculations and data analysis.
Examples and Practice Problems
To solidify your understanding, let's look at some examples and practice problems.
Example 1: Convert 3 1/4 to a decimal.
- Identify the Whole Number: 3
- Convert the Fraction to a Decimal: 1/4 = 0.25 (1 ÷ 4 = 0.25)
- Combine the Whole Number and Decimal: 3 + 0.25 = 3.25
So, 3 1/4 = 3.25.
Example 2: Convert 1 3/5 to a decimal.
- Identify the Whole Number: 1
- Convert the Fraction to a Decimal: 3/5 = 0.6 (3 ÷ 5 = 0.6)
- Combine the Whole Number and Decimal: 1 + 0.6 = 1.6
So, 1 3/5 = 1.6.
Practice Problems:
Convert the following mixed numbers to decimals:
- 4 1/2
- 2 3/4
- 5 1/5
- 3 2/5
Solutions:
- 4 1/2 = 4.5
- 2 3/4 = 2.75
- 5 1/5 = 5.2
- 3 2/5 = 3.4
Common Mistakes to Avoid
When converting mixed numbers to decimals, there are a few common mistakes to watch out for:
- Incorrect Division: Ensure you divide the numerator by the denominator correctly.
- Forgetting the Whole Number: Don't forget to add the whole number to the decimal equivalent of the fraction.
- Misunderstanding Place Value: Make sure you understand the place value system to avoid misplacing the decimal point.
Advanced Concepts
For those looking to deepen their understanding, here are some advanced concepts related to converting mixed numbers to decimals.
Repeating Decimals
Some fractions, when converted to decimals, result in repeating decimals. For example, 1/3 = 0.333... (the 3 repeats infinitely). These are known as repeating decimals or recurring decimals. To represent them, we often use a bar over the repeating digit or digits. For example, 0.333... is written as 0.3.
Converting Repeating Decimals to Fractions
It's also possible to convert repeating decimals back to fractions. This involves a bit of algebra. For example, to convert 0.3 to a fraction:
- Let x = 0.3
- Multiply both sides by 10: 10x = 3.3
- Subtract the original equation from the new equation: 10x - x = 3.3 - 0.3
- Simplify: 9x = 3
- Solve for x: x = 3/9 = 1/3
Irrational Numbers
Some numbers, like pi (π) and the square root of 2 (√2), are irrational numbers. These numbers cannot be expressed as a fraction and have non-repeating, non-terminating decimal representations.
The Role of Technology
In today's world, technology can greatly assist with converting mixed numbers to decimals. Calculators and online converters can quickly and accurately perform these conversions. However, understanding the underlying principles is still essential. Technology should be used as a tool to enhance understanding, not replace it.
Tips for Mastering Conversions
Here are some tips to help you master converting mixed numbers to decimals:
- Practice Regularly: The more you practice, the better you'll become at converting mixed numbers to decimals.
- Memorize Common Conversions: Knowing common fraction-to-decimal conversions can save time.
- Understand the Concepts: Make sure you understand the underlying principles of the decimal system and fractions.
- Use Visual Aids: Visual aids like number lines can help you visualize the relationship between fractions and decimals.
- Check Your Work: Always double-check your work to ensure accuracy.
Conclusion
Converting the mixed number 2 1/2 to a decimal is a straightforward process once you understand the underlying principles. By following the steps outlined in this article, you can confidently convert any mixed number to its decimal equivalent. Remember to practice regularly and use technology as a tool to enhance your understanding. Mastering this skill will not only improve your math skills but also provide you with a valuable tool for various practical applications in everyday life. Whether you're cooking, building, or managing finances, the ability to convert mixed numbers to decimals is a skill that will serve you well.
Latest Posts
Latest Posts
-
What Is 15 Out Of 20
Dec 05, 2025
-
What Is 02 As A Percentage
Dec 05, 2025
-
What Is 40 60 As A Percent
Dec 05, 2025
-
What Is The Decimal For 2 1 2
Dec 05, 2025
-
1 1 8 As A Decimal
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal For 2 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.