What Is 40/60 As A Percent
bemquerermulher
Dec 05, 2025 · 8 min read
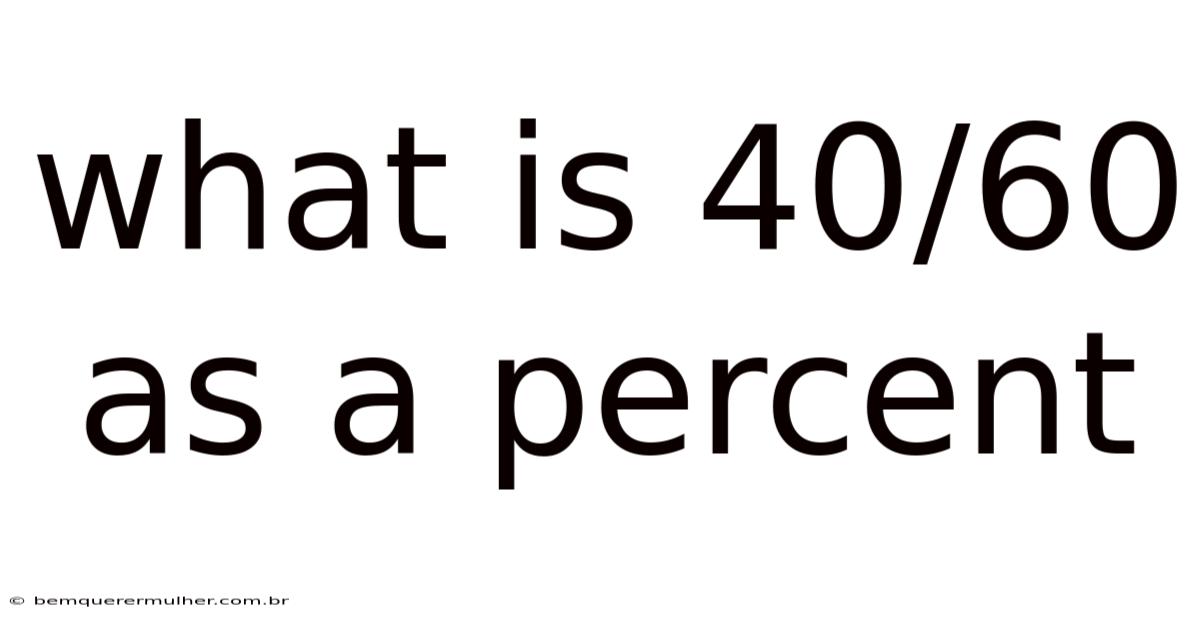
Table of Contents
Converting 40/60 to a percentage is a common mathematical task that arises in various real-life situations, from calculating grades to understanding proportions. A percentage is simply a way of expressing a number as a fraction of 100. Therefore, to convert 40/60 to a percentage, we need to find out what fraction of 100 it represents. This involves a few straightforward steps that we'll explore in detail.
Introduction
Percentages are ubiquitous in daily life. They help us understand proportions, compare values, and make informed decisions. Whether you're figuring out a discount at a store, calculating your exam scores, or understanding statistical data, percentages provide a clear and standardized way to represent numbers.
Converting a fraction like 40/60 to a percentage is a fundamental skill. In this article, we will cover the step-by-step process of converting 40/60 to a percentage, explain the underlying mathematical principles, provide practical examples, and address common questions to help you master this concept.
Understanding Fractions and Percentages
Before diving into the conversion process, it’s important to understand what fractions and percentages represent.
- Fraction: A fraction represents a part of a whole. It is written as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). In the fraction 40/60:
- 40 is the numerator, representing the part.
- 60 is the denominator, representing the whole.
- Percentage: A percentage is a way of expressing a number as a fraction of 100. The term "percent" means "per hundred." For example, 50% means 50 out of 100.
The goal is to express the fraction 40/60 in terms of a fraction with a denominator of 100, which will then directly give us the percentage.
Step-by-Step Conversion of 40/60 to a Percentage
Here’s a detailed, step-by-step guide to converting the fraction 40/60 to a percentage:
Step 1: Simplify the Fraction (If Possible)
Simplifying the fraction makes the subsequent calculations easier. Look for common factors between the numerator and the denominator. In the case of 40/60, both numbers are divisible by 20.
-
Divide both the numerator and the denominator by 20:
- 40 ÷ 20 = 2
- 60 ÷ 20 = 3
So, the simplified fraction is 2/3.
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator.
-
Divide 2 by 3:
- 2 ÷ 3 ≈ 0.6667 (rounded to four decimal places)
The decimal equivalent of 2/3 is approximately 0.6667.
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100.
-
Multiply 0.6667 by 100:
- 0.6667 × 100 = 66.67
Therefore, 40/60 as a percentage is approximately 66.67%.
Alternative Method: Direct Conversion
Another method to convert 40/60 to a percentage involves directly converting the original fraction to a percentage without simplifying it first.
Step 1: Convert the Fraction to a Decimal
Divide the numerator by the denominator.
-
Divide 40 by 60:
- 40 ÷ 60 ≈ 0.6667 (rounded to four decimal places)
Step 2: Convert the Decimal to a Percentage
Multiply the decimal by 100.
-
Multiply 0.6667 by 100:
-
- 6667 × 100 = 66.67
-
As you can see, both methods yield the same result: approximately 66.67%.
Understanding the Math Behind the Conversion
The conversion from a fraction to a percentage is based on the fundamental principle of proportions. A percentage is essentially a ratio expressed as a fraction of 100. When we convert 40/60 to a percentage, we are finding an equivalent ratio with a denominator of 100.
Mathematically, this can be represented as:
(40 / 60) = (x / 100)
To solve for x (which represents the percentage), we can use cross-multiplication:
40 * 100 = 60 * x
4000 = 60x
x = 4000 / 60
x ≈ 66.67
This confirms that 40/60 is approximately 66.67% when expressed as a percentage.
Practical Examples of Percentage Conversion
To further illustrate the concept, let's look at some practical examples where converting fractions to percentages is useful.
Example 1: Calculating Exam Scores
Suppose you scored 40 out of 60 on an exam. To find out your percentage score:
- Fraction of marks obtained: 40/60
- Convert to percentage: (40/60) * 100 ≈ 66.67%
This means you scored approximately 66.67% on the exam.
Example 2: Determining Proportions in a Survey
In a survey, 40 out of 60 respondents preferred a particular product. To express this preference as a percentage:
- Fraction of respondents: 40/60
- Convert to percentage: (40/60) * 100 ≈ 66.67%
This indicates that approximately 66.67% of the respondents preferred the product.
Example 3: Calculating Discounts
If a store offers a discount where you save $40 on an item originally priced at $60, to find the percentage discount:
- Fraction of discount: 40/60
- Convert to percentage: (40/60) * 100 ≈ 66.67%
This means you are getting approximately a 66.67% discount on the item.
Common Mistakes to Avoid
When converting fractions to percentages, it’s important to avoid common errors that can lead to incorrect results. Here are a few to watch out for:
- Incorrect Division: Ensure you divide the numerator by the denominator correctly. Recheck your calculations if the result seems off.
- Forgetting to Multiply by 100: The final step of multiplying the decimal by 100 is crucial. Omitting this step will give you the decimal equivalent, not the percentage.
- Rounding Errors: When rounding decimals, be consistent and use an appropriate number of decimal places to maintain accuracy. Rounding too early or too much can affect the final percentage.
- Misunderstanding the Fraction: Make sure you correctly identify the numerator and the denominator. The numerator represents the part, and the denominator represents the whole.
Tips for Accurate Conversions
To ensure accurate conversions from fractions to percentages, consider the following tips:
- Double-Check Your Work: Always review your calculations to catch any errors in division or multiplication.
- Use a Calculator: A calculator can help avoid mistakes, especially when dealing with complex fractions or decimals.
- Simplify First: Whenever possible, simplify the fraction before converting it to a decimal. This can make the division easier and reduce the chance of errors.
- Understand the Context: Knowing the context of the problem can help you interpret the percentage correctly. For example, understanding whether a percentage represents a score, a proportion, or a discount can provide meaningful insights.
- Practice Regularly: The more you practice converting fractions to percentages, the more comfortable and accurate you will become.
Advanced Applications of Percentages
Beyond basic conversions, percentages are used in more advanced mathematical and statistical applications. Here are a few examples:
Compound Interest
Calculating compound interest involves percentages. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
The interest rate r is often given as a percentage, which needs to be converted to a decimal for the calculation.
Statistical Analysis
Percentages are commonly used in statistical analysis to represent proportions and distributions. For example, when analyzing survey data, percentages can be used to describe the distribution of responses across different categories.
Financial Analysis
In financial analysis, percentages are used to calculate growth rates, profit margins, and return on investment (ROI). These metrics help investors and businesses assess performance and make informed decisions.
FAQ: Frequently Asked Questions
Q: How do I convert a percentage back to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 75% to a fraction:
- 75% = 75/100
- Simplify: 75/100 = 3/4
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a value to a base that has increased. For example, if a company's revenue doubles, the growth is 100%. If it more than doubles, the growth will be more than 100%.
Q: Why are percentages useful?
A: Percentages are useful because they provide a standardized way to express proportions and compare values. They are easy to understand and widely used in various fields, making communication and analysis more straightforward.
Q: What is the difference between a percentage and a percentile?
A: A percentage represents a proportion out of 100, while a percentile indicates the value below which a given percentage of observations in a group of observations falls. For example, if you score in the 80th percentile on a test, it means you scored higher than 80% of the test-takers.
Q: How do I calculate the percentage increase or decrease?
A: To calculate the percentage increase or decrease:
- Find the difference between the new value and the original value.
- Divide the difference by the original value.
- Multiply the result by 100.
Formula:
Percentage Change = ((New Value - Original Value) / Original Value) * 100
Conclusion
Converting 40/60 to a percentage involves simplifying the fraction (if possible), converting it to a decimal, and then multiplying by 100. The result, approximately 66.67%, provides a clear way to understand the proportion represented by the fraction.
Percentages are fundamental in various fields, from calculating scores to understanding proportions in surveys and determining discounts. By mastering the conversion process and understanding the underlying principles, you can confidently apply percentages in everyday situations and advanced applications. Avoiding common mistakes, practicing regularly, and using tools like calculators can further enhance your accuracy and understanding.
Latest Posts
Latest Posts
-
Convert 4 1 2 To A Decimal
Dec 05, 2025
-
What Is The 10 Of 200
Dec 05, 2025
-
What Is 15 Out Of 20
Dec 05, 2025
-
What Is 02 As A Percentage
Dec 05, 2025
-
What Is 40 60 As A Percent
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 40/60 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.