30 Out Of 40 As A Percentage
bemquerermulher
Dec 04, 2025 · 7 min read
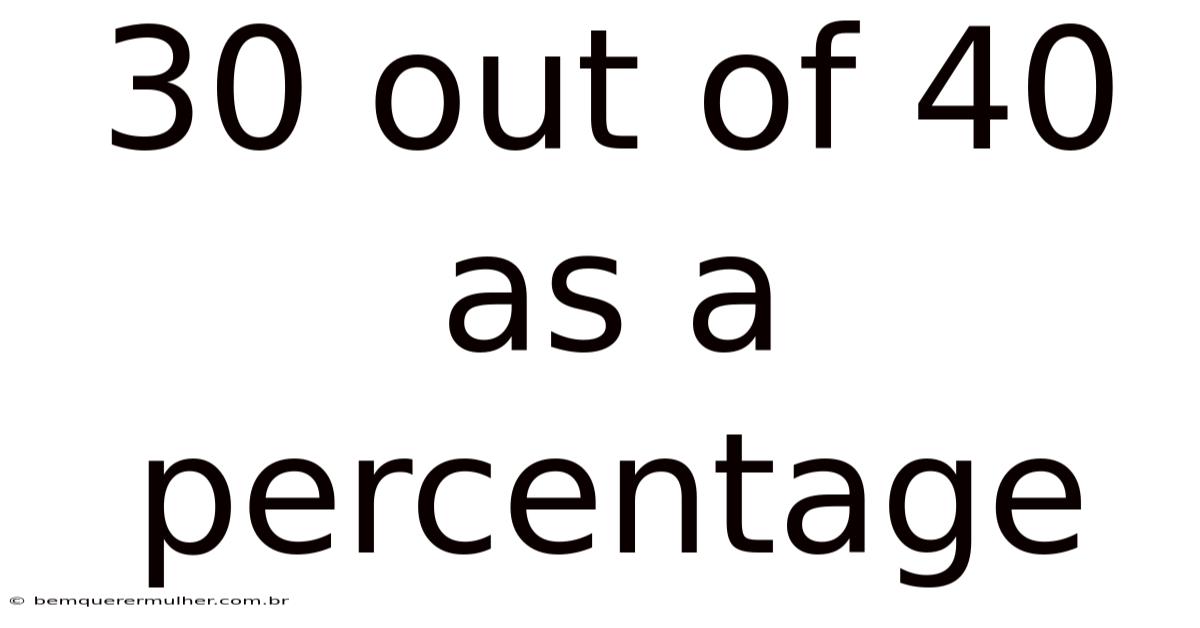
Table of Contents
Calculating percentages is a fundamental skill in mathematics, applicable in various real-life situations, from calculating grades to determining discounts. Understanding how to convert a fraction to a percentage, such as expressing "30 out of 40" as a percentage, is particularly useful. This article provides a detailed explanation of how to perform this calculation, along with practical examples and additional insights to enhance your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." Percentages are used to express how large one quantity is relative to another quantity. To find a percentage, you essentially determine what portion of 100 the number represents.
Basic Formula for Percentage
The basic formula to calculate a percentage is:
Percentage = (Part / Whole) * 100
- Part: This is the specific amount you are interested in.
- Whole: This is the total amount or the reference value.
Step-by-Step Calculation: 30 out of 40 as a Percentage
To express 30 out of 40 as a percentage, follow these steps:
Step 1: Identify the Part and the Whole
In this scenario:
- Part = 30
- Whole = 40
Step 2: Apply the Percentage Formula
Use the formula:
Percentage = (Part / Whole) * 100
Substitute the values:
Percentage = (30 / 40) * 100
Step 3: Perform the Division
Divide 30 by 40:
30 / 40 = 0.75
Step 4: Multiply by 100
Multiply the result by 100 to convert it to a percentage:
- 75 * 100 = 75
Therefore, 30 out of 40 as a percentage is 75%.
Detailed Example with Explanation
Let's break down the calculation with a detailed explanation:
-
Fraction Representation: First, represent the relationship as a fraction: 30/40.
-
Simplify the Fraction (Optional): Simplifying the fraction can make the division easier. Both 30 and 40 are divisible by 10:
30/40 = (30 ÷ 10) / (40 ÷ 10) = 3/4
-
Convert to Decimal: Divide the numerator by the denominator:
3 / 4 = 0.75
-
Convert to Percentage: Multiply the decimal by 100:
- 75 * 100 = 75%
Thus, 30 out of 40 is equivalent to 75%.
Real-World Applications
Understanding how to calculate percentages is useful in numerous real-world scenarios. Here are a few examples:
Example 1: Calculating Grades
Suppose a student scores 30 out of 40 on a test. To find the student's grade as a percentage:
Percentage = (30 / 40) * 100 = 75%
The student's grade is 75%.
Example 2: Determining Discounts
If an item originally priced at $40 is on sale for $30, you can calculate the discount percentage:
-
Calculate the Discount Amount:
Discount Amount = Original Price - Sale Price
Discount Amount = $40 - $30 = $10
-
Calculate the Discount Percentage:
Discount Percentage = (Discount Amount / Original Price) * 100
Discount Percentage = (10 / 40) * 100 = 25%
The discount is 25%.
Example 3: Analyzing Sales Data
A company sold 30 out of 40 products in a week. To find the sales rate as a percentage:
Sales Rate = (30 / 40) * 100 = 75%
The company sold 75% of its products that week.
Tips for Accurate Percentage Calculations
- Double-Check Your Numbers: Ensure you have the correct values for the part and the whole.
- Simplify Fractions: Simplifying fractions before dividing can make the calculation easier and reduce errors.
- Use a Calculator: For complex calculations, use a calculator to ensure accuracy.
- Understand the Context: Always consider the context of the problem to ensure the percentage calculation makes sense.
Common Mistakes to Avoid
- Incorrectly Identifying Part and Whole: Make sure you correctly identify which number is the part and which is the whole. Confusing these can lead to incorrect percentage calculations.
- Forgetting to Multiply by 100: After dividing the part by the whole, remember to multiply by 100 to convert the decimal to a percentage.
- Rounding Errors: Be mindful of rounding errors, especially in intermediate steps. It's best to keep calculations precise until the final step.
Advanced Concepts Related to Percentages
Percentage Increase and Decrease
Understanding percentage increase and decrease is crucial in many applications.
-
Percentage Increase: The formula for percentage increase is:
Percentage Increase = [(New Value - Original Value) / Original Value] * 100
-
Percentage Decrease: The formula for percentage decrease is:
Percentage Decrease = [(Original Value - New Value) / Original Value] * 100
Calculating Percentage Change
Percentage change is a broader term that encompasses both percentage increase and decrease. It is used to describe the relative change in a quantity.
Percentage Change = [(New Value - Original Value) / Original Value] * 100
The result can be positive (increase) or negative (decrease).
Weighted Averages
In some cases, you may need to calculate a weighted average, where different values are given different weights or importance.
Weighted Average = Σ (Value * Weight) / Σ Weight
For example, if you have two test scores: 80% with a weight of 60% and 90% with a weight of 40%, the weighted average is:
Weighted Average = (80 * 0.60) + (90 * 0.40) = 48 + 36 = 84%
Examples of Percentage Calculations in Different Fields
Finance
In finance, percentages are used to calculate interest rates, investment returns, and profit margins. For instance, if an investment of $1,000 yields a profit of $50, the return on investment (ROI) is:
ROI = (50 / 1000) * 100 = 5%
Statistics
In statistics, percentages are used to describe proportions and distributions. For example, if a survey of 200 people finds that 80 prefer coffee over tea, the percentage of people who prefer coffee is:
Percentage = (80 / 200) * 100 = 40%
Retail
Retailers use percentages to calculate discounts, markups, and sales tax. If an item is marked up by 20% from its cost of $50, the selling price is:
Markup Amount = 20% of $50 = 0.20 * 50 = $10
Selling Price = Cost + Markup Amount = $50 + $10 = $60
Tools for Calculating Percentages
- Calculators: Standard calculators have a percentage function that simplifies percentage calculations.
- Spreadsheet Software: Programs like Microsoft Excel and Google Sheets can perform complex percentage calculations and create visualizations.
- Online Percentage Calculators: Numerous websites offer free percentage calculators for quick and easy calculations.
Importance of Understanding Percentages
Understanding percentages is essential for:
- Making Informed Decisions: Whether it's evaluating financial investments or understanding statistical data, percentages help in making informed decisions.
- Budgeting and Finance: Calculating percentages is crucial for managing personal finances, budgeting, and understanding interest rates.
- Academic Success: Percentages are a fundamental part of mathematics and are used in various academic subjects.
- Professional Growth: Many professions require a solid understanding of percentages, from finance and marketing to science and engineering.
Additional Practice Problems
To reinforce your understanding, try these practice problems:
-
Problem: What is 60 out of 80 as a percentage?
- Solution:
Percentage = (60 / 80) * 100 = 75%
-
Problem: If you scored 25 out of 50 on a quiz, what is your score as a percentage?
- Solution:
Percentage = (25 / 50) * 100 = 50%
-
Problem: A store is offering a 15% discount on an item priced at $120. What is the discount amount?
- Solution:
Discount Amount = 15% of $120 = 0.15 * 120 = $18
-
Problem: If a company's revenue increased from $500,000 to $600,000, what is the percentage increase?
- Solution:
Percentage Increase = [(600,000 - 500,000) / 500,000] * 100 = (100,000 / 500,000) * 100 = 20%
The Role of Percentages in Everyday Life
Percentages play a pivotal role in our daily lives, often without us even realizing it. From understanding the nutritional information on food labels to interpreting economic data, percentages provide a standardized way to compare and understand relative quantities.
In Health and Nutrition
Food labels use percentages to indicate the Daily Value (DV) of nutrients in a serving. For example, a label might state that a serving of cereal provides 20% of the recommended daily intake of fiber. This helps consumers make informed choices about their diet.
In Economics and Finance
Economic indicators, such as inflation rates, unemployment rates, and GDP growth, are often expressed as percentages. These figures help economists, policymakers, and the public understand the state of the economy and make informed decisions.
In Politics and Social Sciences
Polls and surveys use percentages to report the proportion of respondents who hold a particular opinion or support a particular candidate. This helps in understanding public sentiment and predicting election outcomes.
In Technology
Percentages are used in various technological applications, such as measuring battery life, data compression rates, and algorithm accuracy.
Conclusion
Expressing 30 out of 40 as a percentage involves a straightforward calculation: (30 / 40) * 100 = 75%. Understanding how to calculate percentages is a valuable skill that applies to many areas of life, including academics, finance, and everyday decision-making. By mastering this fundamental concept, you can improve your analytical skills and make more informed choices. Remember to double-check your numbers, simplify fractions when possible, and use a calculator for complex calculations to ensure accuracy. With practice, you'll become proficient in calculating percentages and using them effectively in various contexts.
Latest Posts
Latest Posts
-
How Tall Is 63 Inches In Feet
Dec 04, 2025
-
How Many Feet Is 52 Inches
Dec 04, 2025
-
How Many Ounces Is 150 Ml
Dec 04, 2025
-
18 Out Of 20 As A Percentage
Dec 04, 2025
-
30 Out Of 40 As A Percentage
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about 30 Out Of 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.