18 Out Of 20 As A Percentage
bemquerermulher
Dec 04, 2025 · 10 min read
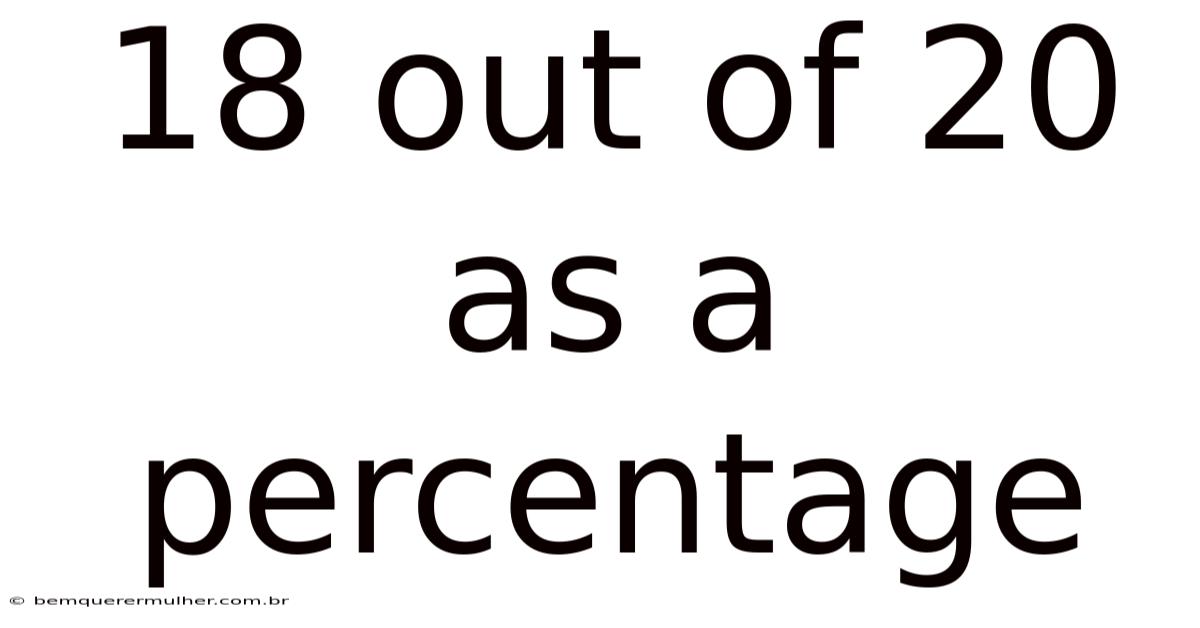
Table of Contents
Here’s how to calculate 18 out of 20 as a percentage, and why understanding percentages is useful in everyday life. We’ll cover the basic formula, step-by-step instructions, and practical examples to make the concept clear and easy to understand.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Percentages are used to express how large one quantity is relative to another quantity. They are a standardized way to compare different ratios, making it easier to understand proportions and rates. In simple terms, percentages tell us how much of something we have if we imagine the whole thing is divided into 100 equal parts.
Percentages are incredibly useful in a variety of real-world scenarios. Here are a few examples:
- Calculating Grades: Teachers often use percentages to represent student performance on tests and assignments. A percentage gives a quick and easily understandable measure of how well a student has performed.
- Retail Discounts: Stores use percentages to show discounts on products. For example, a "20% off" sale tells you that the price is reduced by 20 out of every 100 parts of the original price.
- Financial Analysis: Percentages are used to calculate interest rates on loans and investments. They help you understand the cost of borrowing money or the return on your investments.
- Statistics: Polls and surveys often use percentages to represent the proportion of people who hold a particular opinion or preference.
- Cooking: Recipes sometimes use percentages to describe the proportion of ingredients. This is especially useful in baking, where precise ratios are crucial.
- Health and Fitness: Percentages are used to calculate body fat percentage, daily caloric intake, and other health metrics.
Understanding percentages allows you to quickly interpret and compare different values, make informed decisions, and analyze information effectively.
The Basic Formula for Calculating Percentages
To calculate a percentage, you use a simple formula:
Percentage = (Part / Whole) * 100
- Part: This is the specific quantity you are interested in.
- Whole: This is the total quantity or the reference value.
- Percentage: This is the value you get after applying the formula, expressed as a percentage.
In the case of "18 out of 20," 18 is the part, and 20 is the whole.
Step-by-Step Calculation: 18 out of 20 as a Percentage
Here’s how to calculate what percentage 18 is of 20, broken down into simple steps:
- Identify the Part and the Whole:
- Part = 18
- Whole = 20
- Apply the Formula:
- Percentage = (18 / 20) * 100
- Divide the Part by the Whole:
- 18 / 20 = 0.9
- Multiply by 100:
-
- 9 * 100 = 90
-
- Add the Percentage Sign:
- The result is 90%
So, 18 out of 20 as a percentage is 90%.
Alternative Methods for Calculation
Besides the direct formula, there are a couple of alternative methods you can use to calculate percentages, which can be helpful in different situations:
- Using Fractions to Simplify:
- Sometimes, you can simplify the fraction before converting it to a percentage.
- For example, 18/20 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2.
- 18 ÷ 2 = 9
- 20 ÷ 2 = 10
- So, the simplified fraction is 9/10.
- Now, you can easily convert this to a percentage by multiplying by 100:
- (9/10) * 100 = 90%
- Using Proportions:
- You can set up a proportion to solve for the percentage. A proportion is an equation stating that two ratios are equal.
- The proportion can be set up as follows:
- 18/20 = x/100
- Here, x represents the percentage we want to find.
- To solve for x, you can cross-multiply:
- 18 * 100 = 20 * x
- 1800 = 20x
- Now, divide both sides by 20 to isolate x:
- x = 1800 / 20
- x = 90
- So, the percentage is 90%.
Real-World Examples and Applications
Understanding how to calculate percentages is useful in many everyday situations. Here are a few more detailed examples:
- Calculating Test Scores:
- Imagine you took a test with 20 questions, and you answered 18 of them correctly.
- To find your score as a percentage, you would calculate (18 / 20) * 100 = 90%.
- This means you scored 90% on the test.
- If you want to know how many marks you lost, you can calculate it as 100 - 90 = 10%.
- Discounts and Sales:
- Suppose an item you want to buy is priced at $20, and it’s on sale for $18.
- To find out what percentage of the original price you are paying, you calculate (18 / 20) * 100 = 90%.
- This means you are paying 90% of the original price.
- To find the discount percentage, you calculate 100% - 90% = 10%.
- So, you are getting a 10% discount.
- Budgeting:
- Let’s say you have a budget of $20 for entertainment, and you spend $18 on a movie.
- To determine what percentage of your entertainment budget you spent, you calculate (18 / 20) * 100 = 90%.
- This means you spent 90% of your entertainment budget on the movie.
- You have 100% - 90% = 10% of your budget remaining.
- Tracking Progress:
- If you are trying to read a book with 20 chapters, and you have read 18 chapters, you can calculate your progress as a percentage.
- Progress = (18 / 20) * 100 = 90%.
- This means you have completed 90% of the book.
- Comparing Data:
- Suppose two different classes took a quiz. In Class A, 18 out of 20 students passed. In Class B, 22 out of 25 students passed.
- To compare which class performed better, you need to calculate the percentages.
- Class A: (18 / 20) * 100 = 90%
- Class B: (22 / 25) * 100 = 88%
- Even though more students passed in Class B (22 vs. 18), Class A had a higher percentage of students passing (90% vs. 88%).
Common Mistakes to Avoid
When calculating percentages, it’s easy to make a few common mistakes. Here are some to watch out for:
- Misidentifying the Part and the Whole:
- One of the most common mistakes is confusing the part and the whole. Always make sure you know which value represents the total amount (the whole) and which value represents the specific portion you are interested in (the part).
- For example, if you are calculating what percentage of your monthly income you spend on rent, your rent payment is the part, and your total monthly income is the whole.
- Incorrectly Applying the Formula:
- Make sure you are following the correct formula:
Percentage = (Part / Whole) * 100. - Sometimes, people forget to multiply by 100, which will give you a decimal value instead of a percentage.
- Make sure you are following the correct formula:
- Rounding Errors:
- When dividing the part by the whole, you might get a decimal number. If you round this number before multiplying by 100, it can lead to inaccuracies in the final percentage.
- It’s better to keep as many decimal places as possible until the final step, and then round the final percentage if necessary.
- Forgetting Units:
- Always remember that a percentage is a ratio out of 100. It’s important to include the percentage sign (%) in your final answer to indicate that it’s a percentage and not just a regular number.
- Assuming the Whole is Always 100:
- The whole is not always 100 unless you are specifically working with percentages in reverse to find the original whole. The whole is simply the total quantity you are using as a reference.
Advanced Tips and Tricks
Here are some advanced tips and tricks for working with percentages:
- Calculating Percentage Change:
- To find the percentage change between two values (an initial value and a final value), you can use the following formula:
Percentage Change = ((Final Value - Initial Value) / Initial Value) * 100
- For example, if a stock's price increased from $50 to $60, the percentage change would be:
Percentage Change = (($60 - $50) / $50) * 100 = (10 / 50) * 100 = 20%
- This means the stock's price increased by 20%.
- To find the percentage change between two values (an initial value and a final value), you can use the following formula:
- Working with Multiple Percentages:
- When dealing with multiple percentages (e.g., successive discounts or taxes), be careful about applying them sequentially.
- For example, if an item is discounted by 20% and then an additional 10%, you can’t simply add the percentages to get a 30% discount.
- Instead, calculate each discount separately:
- Original price: $100
- 20% discount: $100 * 0.20 = $20
- Price after 20% discount: $100 - $20 = $80
- 10% discount on $80: $80 * 0.10 = $8
- Final price: $80 - $8 = $72
- The total discount is $100 - $72 = $28, which is 28% of the original price, not 30%.
- Using Percentages in Reverse:
- Sometimes, you might know the percentage and need to find the original whole.
- For example, if you know that $30 is 25% of your total budget, you can find the total budget by setting up the equation:
0. 25 * Total Budget = $30Total Budget = $30 / 0.25 = $120
- So, your total budget is $120.
- Estimating Percentages Quickly:
- To quickly estimate percentages, you can use benchmarks like 10%, 25%, 50%, and 75%.
- For example, to find 10% of a number, simply move the decimal point one place to the left.
- To find 25%, divide the number by 4.
- To find 50%, divide the number by 2.
- To find 75%, divide the number by 4 and then multiply by 3.
The History of Percentages
The concept of percentages has ancient roots. The Romans used fractions similar to percentages, often based on hundredths. For example, Emperor Augustus levied a tax of 1/100 on goods sold at auction, known as centesima rerum venalium.
However, the modern concept of percentages as we know it today emerged during the Renaissance. As trade and commerce grew, there was an increasing need for a standardized way to calculate interest, taxes, and profits. The explicit use of the percent sign (%) developed over time. In the 15th century, Italian texts used terms like "per cento" or "per cento." By the 17th century, the term had evolved to "percent."
The percent sign (%) is believed to have evolved from the Italian abbreviation "pc" for per cento. Over time, the "pc" evolved into a symbol with a horizontal line between two circles, which eventually became the percentage sign we use today.
The standardization of percentages made financial calculations easier and more transparent, contributing to the growth of modern economies. Today, percentages are an essential tool in finance, statistics, and everyday life.
How to Practice and Improve Your Skills
To become more comfortable and proficient with calculating percentages, here are some practice exercises and tips:
- Practice Problems:
- Try solving various percentage problems regularly. You can find practice problems in textbooks, online resources, or create your own scenarios.
- Start with simple problems and gradually increase the difficulty as you become more confident.
- Real-Life Applications:
- Apply percentage calculations in your daily life. For example, calculate discounts when shopping, estimate tips at restaurants, or track your spending as a percentage of your budget.
- Use Online Tools:
- There are many online percentage calculators and tools that can help you check your work and understand the concepts better.
- These tools can provide instant feedback and help you identify areas where you need more practice.
- Teach Others:
- One of the best ways to reinforce your understanding of percentages is to teach someone else. Explaining the concepts to others can help you identify any gaps in your own knowledge.
- Seek Clarification:
- If you are struggling with a particular concept, don’t hesitate to ask for help. Consult with teachers, tutors, or online forums to get clarification and additional explanations.
Conclusion
Calculating 18 out of 20 as a percentage is a straightforward process that involves dividing 18 by 20 and then multiplying by 100, resulting in 90%. Understanding percentages is a crucial skill that applies to many aspects of daily life, from calculating grades and discounts to managing finances and interpreting statistics. By mastering the basic formula and practicing regularly, you can confidently use percentages to make informed decisions and analyze information effectively. Avoiding common mistakes and exploring advanced techniques will further enhance your proficiency.
Latest Posts
Latest Posts
-
How Tall Is 63 Inches In Feet
Dec 04, 2025
-
How Many Feet Is 52 Inches
Dec 04, 2025
-
How Many Ounces Is 150 Ml
Dec 04, 2025
-
18 Out Of 20 As A Percentage
Dec 04, 2025
-
30 Out Of 40 As A Percentage
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about 18 Out Of 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.