What Percent Is 20 Of 150
bemquerermulher
Dec 05, 2025 · 7 min read
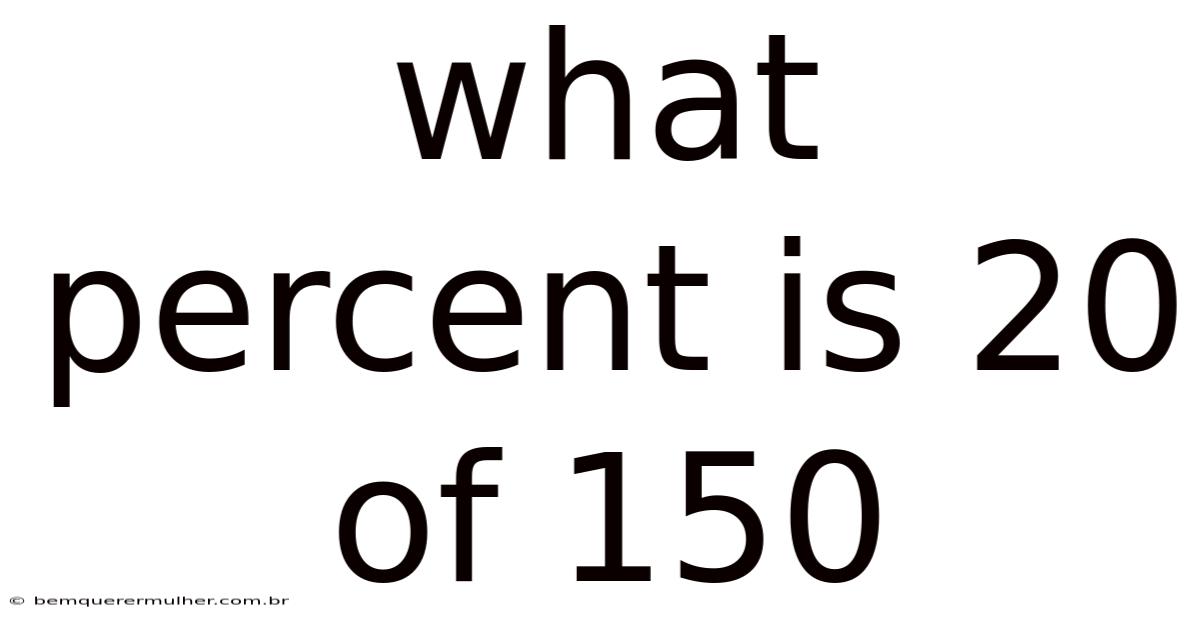
Table of Contents
Twenty is what percent of 150? This question involves calculating percentages, a fundamental skill applicable in many real-world situations, from finance and shopping to scientific analysis. Understanding how to find what percentage one number is of another helps in interpreting data, making informed decisions, and solving practical problems. This article will guide you through the steps to accurately determine the percentage and offer insights into why this calculation is significant.
Understanding Percentages
The term percent comes from the Latin per centum, meaning "per hundred." A percentage is a way of expressing a number as a fraction of 100. It is a dimensionless number, meaning it is just a ratio without any units. Percentages are used to express how large one quantity is relative to another quantity.
Basic Formula for Percentage Calculation
To find what percentage one number (the part) is of another number (the whole), you use the following formula:
$\text{Percentage} = \left( \frac{\text{Part}}{\text{Whole}} \right) \times 100$
In this formula:
- Part is the value you want to express as a percentage of another value.
- Whole is the total or reference value.
Step-by-Step Calculation: What Percent is 20 of 150?
Here’s how to apply the formula to find what percentage 20 is of 150:
Step 1: Identify the Part and the Whole
In the question "What percent is 20 of 150?", identify which number is the part and which is the whole.
- Part: 20
- Whole: 150
Step 2: Apply the Percentage Formula
Use the formula to calculate the percentage:
$\text{Percentage} = \left( \frac{20}{150} \right) \times 100$
Step 3: Perform the Division
First, divide the part (20) by the whole (150):
$\frac{20}{150} = 0.1333$
The result is a decimal number.
Step 4: Multiply by 100
To convert the decimal to a percentage, multiply by 100:
$0.1333 \times 100 = 13.33%$
Therefore, 20 is approximately 13.33% of 150.
Alternative Method: Using Proportion
Another way to solve percentage problems is by using proportions. A proportion is an equation stating that two ratios are equal.
Step 1: Set Up the Proportion
Set up the proportion as follows:
$\frac{\text{Part}}{\text{Whole}} = \frac{\text{Percentage}}{100}$
In this case:
$\frac{20}{150} = \frac{x}{100}$
Here, x represents the percentage we want to find.
Step 2: Solve for x
To solve for x, cross-multiply:
$20 \times 100 = 150 \times x$ $2000 = 150x$
Step 3: Isolate x
Divide both sides by 150 to solve for x:
$x = \frac{2000}{150}$ $x = 13.33$
Thus, 20 is approximately 13.33% of 150.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential in various real-life scenarios:
Finance
In finance, percentages are used to calculate interest rates, investment returns, and discounts. For instance, if you invest $150 and earn $20 in interest, the percentage return on your investment is:
$\text{Percentage Return} = \left( \frac{20}{150} \right) \times 100 = 13.33%$
This allows you to compare the profitability of different investments.
Retail
Retailers use percentages to determine discounts and markups. For example, if an item originally priced at $150 is on sale for $20 off, the discount percentage is:
$\text{Discount Percentage} = \left( \frac{20}{150} \right) \times 100 = 13.33%$
Education
In education, percentages are used to calculate grades and assess student performance. If a student scores 20 out of 150 on a test, their percentage score is:
$\text{Score Percentage} = \left( \frac{20}{150} \right) \times 100 = 13.33%$
This helps in evaluating the student’s understanding of the material.
Statistics
Percentages are widely used in statistics to represent data and compare different groups. For instance, if a survey of 150 people shows that 20 prefer a certain product, the percentage of people who prefer the product is:
$\text{Preference Percentage} = \left( \frac{20}{150} \right) \times 100 = 13.33%$
This can help businesses understand consumer preferences.
Common Mistakes to Avoid
When calculating percentages, it’s important to avoid common mistakes:
Misidentifying the Part and Whole
One of the most frequent errors is confusing the part and the whole. Always ensure that you correctly identify which value you are expressing as a percentage of the other. For example, if the question is "What percent is 150 of 20?", the calculation would be:
$\text{Percentage} = \left( \frac{150}{20} \right) \times 100 = 750%$
Incorrectly Applying the Formula
Ensure you use the correct formula:
$\text{Percentage} = \left( \frac{\text{Part}}{\text{Whole}} \right) \times 100$
Flipping the part and whole will lead to an incorrect result.
Forgetting to Multiply by 100
After dividing the part by the whole, remember to multiply by 100 to convert the decimal to a percentage. Failing to do so will give you a decimal value instead of a percentage.
Rounding Errors
Be cautious with rounding. If you round intermediate values, it can affect the accuracy of your final percentage. It’s best to round only at the final step.
Advanced Tips for Percentage Calculations
Here are some advanced tips to enhance your understanding and calculation of percentages:
Using Percentages to Find the Part
Sometimes you need to find the part when you know the whole and the percentage. Rearrange the formula to solve for the part:
$\text{Part} = \frac{\text{Percentage}}{100} \times \text{Whole}$
For example, if you want to find 13.33% of 150:
$\text{Part} = \frac{13.33}{100} \times 150 = 19.995 \approx 20$
Calculating Percentage Increase or Decrease
To calculate the percentage increase or decrease between two values:
$\text{Percentage Change} = \left( \frac{\text{New Value} - \text{Old Value}}{\text{Old Value}} \right) \times 100$
For example, if a value increases from 150 to 170:
$\text{Percentage Increase} = \left( \frac{170 - 150}{150} \right) \times 100 = \left( \frac{20}{150} \right) \times 100 = 13.33%$
Understanding Percentage Points
Percentage points are used to describe the difference between two percentages. For example, if a rate increases from 10% to 15%, it has increased by 5 percentage points. This is different from a 5% increase, which would be a much smaller change.
Examples and Practice Questions
Let’s work through some examples and practice questions to solidify your understanding of percentage calculations.
Example 1: Finding the Percentage
Question: What percent is 30 of 200? Solution:
$\text{Percentage} = \left( \frac{30}{200} \right) \times 100 = 15%$
Example 2: Calculating a Discount
Question: A shirt costs $80, and there is a discount of $12. What is the discount percentage? Solution:
$\text{Discount Percentage} = \left( \frac{12}{80} \right) \times 100 = 15%$
Example 3: Finding the Part
Question: What is 25% of 300? Solution:
$\text{Part} = \frac{25}{100} \times 300 = 75$
Practice Question 1
What percent is 45 of 250?
Practice Question 2
A store offers a 30% discount on a $120 item. What is the discount amount?
Practice Question 3
If 60 out of 400 students passed an exam, what percentage of students passed?
Why Understanding Percentages is Important
Understanding percentages is not just a mathematical skill; it’s a crucial life skill. Here’s why:
Financial Literacy
Percentages are used in budgeting, investing, and understanding loans and interest rates. Being able to calculate and interpret percentages helps you make informed financial decisions.
Informed Decision-Making
From shopping discounts to understanding statistical data, percentages help you compare values and make rational decisions.
Professional Applications
Many professions, including finance, marketing, and healthcare, rely on percentages for data analysis and reporting.
Everyday Life
Whether it’s calculating tips at a restaurant or understanding nutritional information on food labels, percentages are part of daily life.
Conclusion
In summary, calculating what percentage 20 is of 150 involves dividing 20 by 150 and then multiplying by 100, resulting in approximately 13.33%. This skill is not only a fundamental mathematical concept but also a practical tool for various real-life applications. By understanding the basic formula, avoiding common mistakes, and practicing with examples, you can confidently apply percentage calculations in finance, retail, education, statistics, and beyond. Whether you are calculating investment returns, discounts, grades, or survey results, mastering percentages empowers you to make informed decisions and interpret data effectively.
Latest Posts
Latest Posts
-
How Many Inches Are In 28 Centimeters
Dec 05, 2025
-
How Many Liters In 6 Gallons
Dec 05, 2025
-
The First Trophic Level Consists Of Organisms That What
Dec 05, 2025
-
What Percent Is 20 Of 150
Dec 05, 2025
-
What Is 15 40 As A Percent
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 20 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.