What Is The Percent Of 5/6
bemquerermulher
Dec 05, 2025 · 9 min read
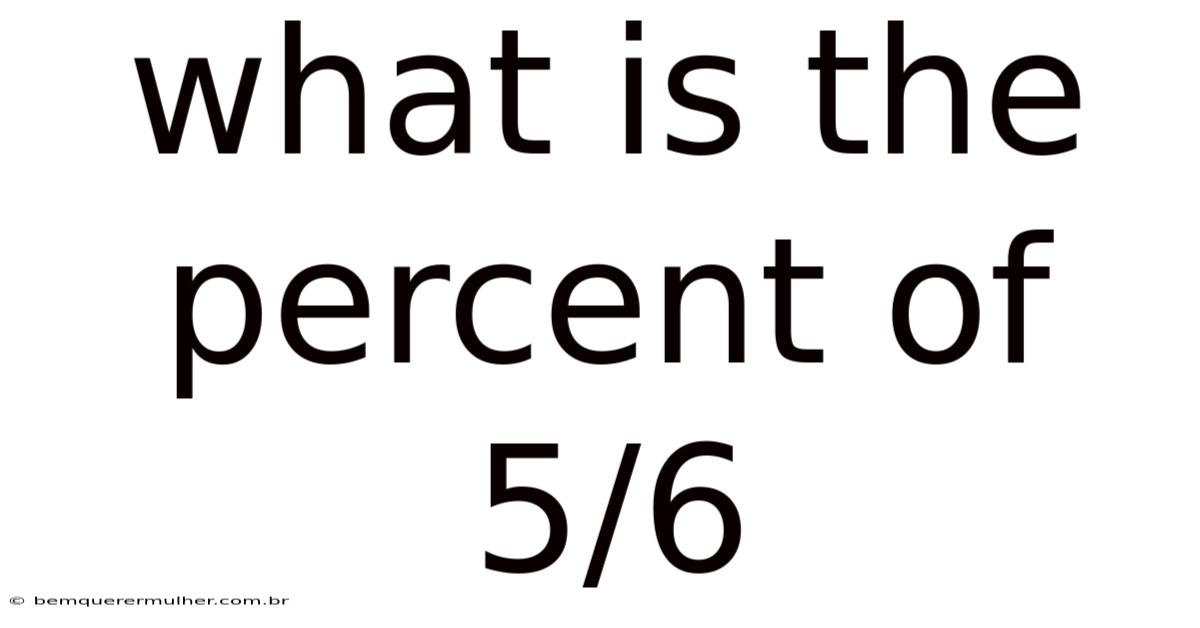
Table of Contents
Understanding Percentages: Calculating the Percent of 5/6
Percentages are a fundamental concept in mathematics and are widely used in various aspects of daily life, from calculating discounts to understanding statistics. A percentage is simply a way of expressing a number as a fraction of 100. When we ask, "What is the percent of 5/6?", we are essentially asking how to express the fraction 5/6 as a percentage. This involves converting the fraction to a decimal and then multiplying by 100 to get the percentage. In this article, we will explore step-by-step methods, practical examples, and the underlying principles to help you understand and calculate the percent of 5/6.
Introduction
Percentages are a crucial part of mathematical literacy. They provide a standardized way to understand proportions and ratios, making it easier to compare different quantities. Converting fractions to percentages is a common task in various fields, including finance, science, and everyday problem-solving. Understanding how to perform this conversion accurately can enhance your ability to interpret data and make informed decisions.
In this article, we will cover:
- The basic definition of percentage and its importance.
- Step-by-step methods to convert the fraction 5/6 into a percentage.
- Practical examples and applications of this conversion.
- The underlying mathematical principles that make this conversion possible.
- Frequently asked questions to clarify common points of confusion.
By the end of this article, you will have a comprehensive understanding of how to calculate the percent of 5/6 and be able to apply this knowledge to other similar problems.
Step-by-Step Method to Calculate the Percent of 5/6
Converting a fraction to a percentage involves a few straightforward steps. By following these steps, you can easily find the percentage equivalent of any fraction.
Step 1: Convert the Fraction to a Decimal
The first step in converting the fraction 5/6 to a percentage is to divide the numerator (5) by the denominator (6). This will give you the decimal equivalent of the fraction.
Calculation: 5 ÷ 6 = 0.8333...
The result is a repeating decimal, approximately 0.8333. For practical purposes, you can round this to a suitable number of decimal places, such as four or five, depending on the required precision.
Step 2: Multiply the Decimal by 100
Once you have the decimal equivalent, the next step is to multiply it by 100. This converts the decimal to a percentage.
Calculation: 0. 8333 × 100 = 83.33%
So, 5/6 as a percentage is approximately 83.33%. The percentage can be rounded to the nearest tenth or hundredth, depending on the level of precision needed.
Step 3: Add the Percent Symbol
The final step is to add the percent symbol (%) to the numerical value. This indicates that the number is a percentage and not a simple decimal or fraction.
Final Answer: 5/6 = 83.33%
Following these three simple steps will allow you to convert any fraction into its percentage equivalent accurately.
Practical Examples and Applications
Understanding how to convert fractions to percentages is valuable in various real-world scenarios. Let's explore some practical examples where knowing the percent of 5/6 might be useful.
Example 1: Calculating Grades
Imagine you scored 5 out of 6 points on a quiz. To find out your grade as a percentage, you would convert 5/6 to a percentage.
Calculation: As we already found, 5/6 is approximately 83.33%. Therefore, your grade on the quiz is 83.33%.
Example 2: Budgeting
Suppose you allocated 5/6 of your monthly budget to essential expenses. To understand what percentage of your budget this represents, you would convert 5/6 to a percentage.
Calculation: 5/6 is approximately 83.33%. This means that 83.33% of your budget is allocated to essential expenses.
Example 3: Sports Statistics
In sports, statistics are often expressed as fractions. For instance, if a basketball player makes 5 out of 6 free throws, you can convert this fraction to a percentage to understand their success rate.
Calculation: 5/6 is approximately 83.33%. This means the player has an 83.33% success rate for free throws.
Example 4: Cooking and Baking
In recipes, proportions are sometimes given as fractions. If a recipe calls for 5/6 of a cup of an ingredient, converting this to a percentage can help you visualize the quantity relative to a full cup.
Calculation: 5/6 is approximately 83.33%. This means you need about 83.33% of a full cup of the ingredient.
These examples illustrate how converting fractions to percentages can provide a more intuitive understanding of proportions in various contexts.
The Underlying Mathematical Principles
To fully understand the conversion of fractions to percentages, it's essential to grasp the underlying mathematical principles.
Definition of Percentage
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." Thus, a percentage is essentially a ratio with a denominator of 100.
Converting Fractions to Decimals
To convert a fraction to a decimal, you divide the numerator by the denominator. This process yields a decimal number that represents the same proportion as the fraction. Formula: Decimal = Numerator / Denominator
Converting Decimals to Percentages
To convert a decimal to a percentage, you multiply the decimal by 100. This is because a percentage is defined as the number of parts per 100. Formula: Percentage = Decimal × 100
Combining the Steps
When converting a fraction to a percentage, you are essentially performing two operations:
- Converting the fraction to a decimal by dividing the numerator by the denominator.
- Converting the decimal to a percentage by multiplying by 100. Combined Formula: Percentage = (Numerator / Denominator) × 100
Why This Works
The reason this method works is rooted in the definition of percentage. By converting the fraction to a decimal, you are finding the equivalent value in decimal form. Multiplying by 100 then scales this decimal value to represent the number of parts per 100, which is precisely what a percentage represents.
Common Mistakes to Avoid
When converting fractions to percentages, there are a few common mistakes that you should be aware of to ensure accuracy.
Mistake 1: Incorrect Division
One of the most common mistakes is dividing the denominator by the numerator instead of dividing the numerator by the denominator. Remember, the correct formula is:
Decimal = Numerator / Denominator
Mistake 2: Forgetting to Multiply by 100
After converting the fraction to a decimal, it's crucial to multiply the decimal by 100 to get the percentage. Forgetting this step will result in an incorrect answer.
Mistake 3: Rounding Errors
When dealing with repeating decimals, rounding errors can occur. It's important to round to an appropriate number of decimal places, depending on the required precision. For most practical purposes, rounding to two decimal places is sufficient.
Mistake 4: Misunderstanding the Concept of Percentage
A basic misunderstanding of what a percentage represents can lead to errors. Always remember that a percentage is a way of expressing a number as a fraction of 100.
Mistake 5: Not Checking Your Answer
It's always a good idea to check your answer, especially in exams or important calculations. You can do this by converting the percentage back to a fraction to see if it matches the original fraction.
By being mindful of these common mistakes, you can improve your accuracy and avoid errors when converting fractions to percentages.
Tips for Accurate Calculations
To ensure your calculations are accurate, here are some helpful tips:
- Use a Calculator: A calculator can help you avoid arithmetic errors, especially when dealing with complex fractions or decimals.
- Double-Check Your Work: Always take a moment to review your calculations to ensure you haven't made any mistakes.
- Understand the Concept: Make sure you have a clear understanding of what a percentage represents and how it relates to fractions and decimals.
- Practice Regularly: The more you practice converting fractions to percentages, the more proficient you will become.
- Use Estimation: Before performing the exact calculation, estimate the answer to get a sense of whether your final result is reasonable. For example, since 5/6 is close to 1, you know the percentage should be close to 100%.
- Write Down Each Step: Clearly writing down each step of the calculation can help you identify and correct any errors you might make along the way.
- Be Mindful of Rounding: When rounding decimals, be consistent and round to an appropriate number of decimal places.
By following these tips, you can improve your accuracy and confidence when working with percentages.
FAQ Section
Here are some frequently asked questions related to converting fractions to percentages, specifically focusing on the fraction 5/6.
Q1: What is the percentage of 5/6? A: The percentage of 5/6 is approximately 83.33%.
Q2: How do you convert 5/6 to a percentage? A: To convert 5/6 to a percentage, divide 5 by 6 to get the decimal equivalent (0.8333) and then multiply by 100 to get 83.33%.
Q3: Why do we multiply by 100 when converting a decimal to a percentage? A: Multiplying by 100 converts the decimal to a percentage because a percentage is defined as the number of parts per 100.
Q4: Can 5/6 be expressed as an exact percentage? A: No, 5/6 cannot be expressed as an exact percentage because the decimal equivalent (0.8333...) is a repeating decimal. Therefore, the percentage is an approximation.
Q5: What are some real-world applications of converting 5/6 to a percentage? A: Real-world applications include calculating grades, understanding budget allocations, interpreting sports statistics, and adjusting recipes in cooking.
Q6: Is it important to round correctly when converting 5/6 to a percentage? A: Yes, it's important to round correctly to maintain accuracy. Rounding to two decimal places (e.g., 83.33%) is often sufficient for most practical purposes.
Q7: What is the formula for converting a fraction to a percentage? A: The formula is: Percentage = (Numerator / Denominator) × 100.
Q8: How can I check if my conversion of 5/6 to a percentage is correct? A: You can check your conversion by converting the percentage back to a fraction. If the result is close to 5/6, your conversion is likely correct.
Q9: What should I do if I keep making mistakes when converting fractions to percentages? A: Practice regularly, use a calculator, double-check your work, and ensure you understand the concept of percentage. If you're still struggling, seek help from a teacher or tutor.
Q10: Can I use a calculator to convert 5/6 to a percentage? A: Yes, using a calculator is highly recommended for accurate and quick conversions, especially for complex fractions.
Conclusion
Converting fractions to percentages is a fundamental skill with numerous applications in everyday life. By following the step-by-step methods outlined in this article, you can easily convert the fraction 5/6 to its percentage equivalent, which is approximately 83.33%. Understanding the underlying mathematical principles and avoiding common mistakes will help you perform these calculations accurately and confidently. Whether you're calculating grades, managing a budget, or interpreting statistics, the ability to convert fractions to percentages is an invaluable asset. With practice and a clear understanding of the concepts, you can master this skill and apply it effectively in various contexts.
Latest Posts
Latest Posts
-
51 Inches Is How Many Feet
Dec 05, 2025
-
1 In 7 As A Percentage
Dec 05, 2025
-
How Many Pounds Are In 58 Kg
Dec 05, 2025
-
How Many Ounces In 2 Lb
Dec 05, 2025
-
What Is The Percent Of 5 6
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 5/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.