What Is The Percent Of 12/20
bemquerermulher
Dec 05, 2025 · 9 min read
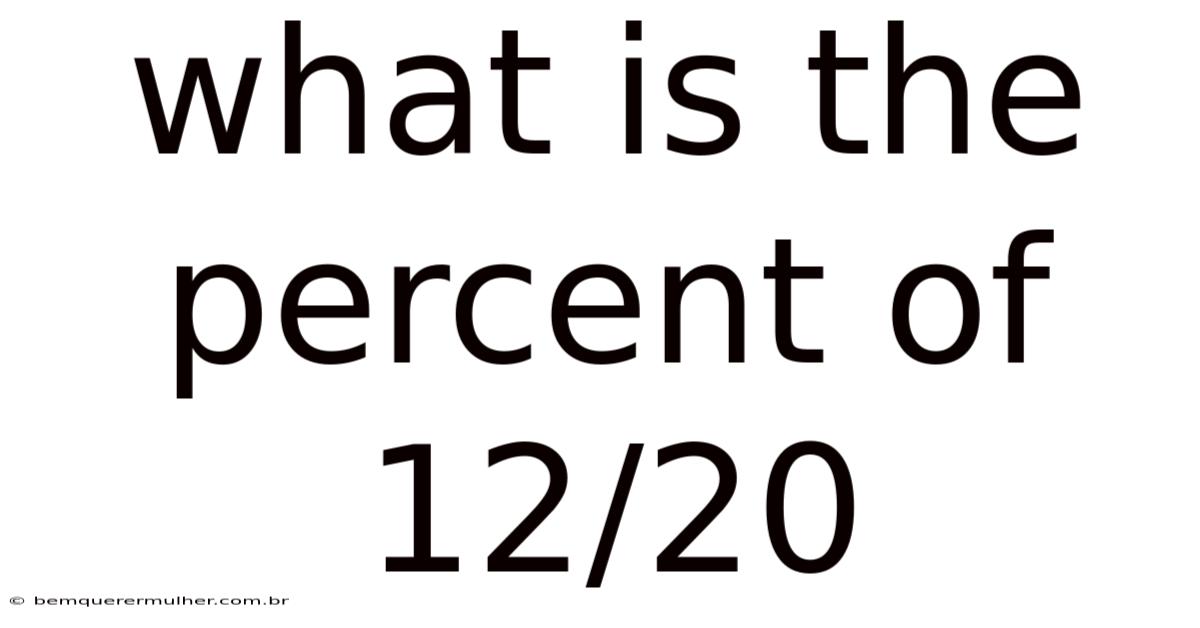
Table of Contents
Converting Fractions to Percentages: A Comprehensive Guide to Determining What Percent 12/20 Is
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications, from everyday calculations to advanced problem-solving. In this comprehensive guide, we will explore the step-by-step process of converting the fraction 12/20 into a percentage, providing a clear and easy-to-follow explanation that suits both students and professionals. By the end of this article, you will not only know what percent 12/20 is, but also understand the underlying principles that allow you to convert any fraction into a percentage with confidence.
Introduction
The concept of percentages is deeply ingrained in our daily lives. We encounter them in financial transactions, statistical analysis, and even in the grading systems of academic institutions. A percentage is essentially a way to express a number as a fraction of 100. It provides a standardized way to compare different quantities, making it easier to understand relative proportions.
Fractions, on the other hand, represent parts of a whole. They consist of two components: the numerator (the number above the fraction bar) and the denominator (the number below the fraction bar). Converting a fraction to a percentage allows us to express this part-to-whole relationship in a more universally understandable format.
In this article, we will focus on the specific fraction 12/20. Our goal is to determine what percentage 12/20 represents. To achieve this, we will break down the conversion process into manageable steps, ensuring that you grasp the concept thoroughly.
Understanding the Basics: Fractions and Percentages
Before diving into the conversion process, let's clarify some fundamental concepts related to fractions and percentages.
- Fraction: A fraction represents a part of a whole. It is written as a/b, where a is the numerator and b is the denominator. The numerator indicates how many parts we have, and the denominator indicates the total number of parts that make up the whole.
- Percentage: A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." A percentage is denoted by the symbol %. For example, 50% means 50 out of 100.
- Conversion: Converting a fraction to a percentage involves transforming the fraction into an equivalent form that is expressed as a value out of 100. This conversion makes it easier to understand and compare different proportions.
Step-by-Step Guide: Converting 12/20 to a Percentage
To convert the fraction 12/20 into a percentage, we can follow these steps:
Step 1: Simplify the Fraction (If Possible)
Simplifying a fraction involves reducing it to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by that number. For the fraction 12/20, the GCD is 4.
- Divide the numerator (12) by 4: 12 ÷ 4 = 3
- Divide the denominator (20) by 4: 20 ÷ 4 = 5
So, the simplified fraction is 3/5.
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator.
- Divide 3 by 5: 3 ÷ 5 = 0.6
Thus, the decimal equivalent of the fraction 3/5 is 0.6.
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%).
- Multiply 0.6 by 100: 0.6 × 100 = 60
Therefore, 0.6 is equal to 60%.
So, 12/20 is equal to 60%.
Alternative Method: Direct Conversion to Percentage
Another method to convert 12/20 to a percentage involves directly manipulating the fraction to have a denominator of 100. Here’s how:
Step 1: Find the Multiplier
Determine what number you need to multiply the denominator (20) by to get 100.
- 20 × ? = 100
- ? = 100 ÷ 20
- ? = 5
So, you need to multiply the denominator by 5 to get 100.
Step 2: Multiply Both Numerator and Denominator
Multiply both the numerator (12) and the denominator (20) by 5.
- Numerator: 12 × 5 = 60
- Denominator: 20 × 5 = 100
The new fraction is 60/100.
Step 3: Express as a Percentage
Since the fraction is now in the form of x/100, the percentage is simply x%.
Therefore, 60/100 is equal to 60%.
Practical Examples and Applications
Understanding how to convert fractions to percentages is valuable in various real-world scenarios. Let's explore some practical examples and applications.
Example 1: Test Scores
Suppose you scored 12 out of 20 on a quiz. To find your score as a percentage:
- Fraction: 12/20
- Convert to Percentage: (12/20) × 100 = 60%
Your score on the quiz is 60%.
Example 2: Sales Discount
A store offers a discount where an item is 12/20 of its original price. To understand the discount as a percentage:
- Fraction of Original Price: 12/20
- Convert to Percentage: (12/20) × 100 = 60%
The item is being sold at 60% of its original price, meaning the discount is 40%.
Example 3: Survey Results
In a survey, 12 out of 20 people preferred a certain product. To express this as a percentage:
- Fraction of People Preferring the Product: 12/20
- Convert to Percentage: (12/20) × 100 = 60%
60% of the people surveyed preferred the product.
Common Mistakes to Avoid
When converting fractions to percentages, it's essential to avoid common mistakes that can lead to incorrect results. Here are some pitfalls to watch out for:
- Incorrect Simplification: Ensure that you correctly simplify the fraction by finding the greatest common divisor (GCD) accurately. An incorrect GCD will lead to an incorrect simplified fraction.
- Division Errors: When converting a fraction to a decimal, make sure you perform the division correctly. Double-check your calculations to avoid errors that can significantly alter the result.
- Misunderstanding the Decimal Point: Ensure you understand the placement of the decimal point. A misplaced decimal can change the value drastically.
- Forgetting to Multiply by 100: One of the most common mistakes is forgetting to multiply the decimal by 100 to convert it to a percentage. Always remember this crucial step.
- Confusing Numerator and Denominator: Always ensure you divide the numerator by the denominator, not the other way around. Confusing these can lead to the wrong result.
The Importance of Understanding Percentages
Understanding percentages is crucial for several reasons:
- Financial Literacy: Percentages are used extensively in finance, from calculating interest rates to understanding investment returns.
- Data Interpretation: Percentages help in interpreting statistical data, making it easier to understand trends and comparisons.
- Decision Making: Whether you're evaluating a discount, comparing prices, or analyzing survey results, percentages provide a clear and concise way to make informed decisions.
- Academic Performance: Many subjects, especially mathematics and science, require a solid understanding of percentages to solve problems and interpret results.
- Everyday Life: From cooking to budgeting, percentages are used in various daily activities, making it an essential skill for everyone.
Advanced Techniques and Tips
While the basic methods are sufficient for most conversions, here are some advanced techniques and tips to enhance your understanding and speed up the process:
- Memorizing Common Fractions: Memorizing the percentage equivalents of common fractions such as 1/2, 1/4, 1/3, and 1/5 can save time and improve accuracy.
- Using Mental Math: Practice mental math techniques to quickly estimate percentages. For example, to find 10% of a number, simply move the decimal point one place to the left.
- Percentage Increase and Decrease: Understand how to calculate percentage increase and decrease, which involves finding the difference between two values and expressing it as a percentage of the original value.
- Using a Calculator: While understanding the underlying principles is important, using a calculator can help when dealing with complex or large numbers.
Scientific Explanation
The process of converting a fraction to a percentage is based on fundamental mathematical principles. A fraction represents a ratio, and a percentage is a standardized way to express this ratio relative to 100.
When we convert a fraction a/b to a percentage, we are essentially finding an equivalent fraction with a denominator of 100. This is achieved by multiplying both the numerator and the denominator by a factor that transforms the denominator into 100. The resulting numerator then represents the percentage.
Mathematically, the conversion can be expressed as:
Percentage = (a/b) × 100%
This formula ensures that we are maintaining the same ratio while expressing it in terms of 100, which is the basis of percentage calculations.
FAQ Section
Here are some frequently asked questions related to converting fractions to percentages:
Q: Why do we multiply by 100 when converting a decimal to a percentage?
A: Multiplying by 100 converts the decimal into a percentage by expressing it as a value out of 100. Since percentages are based on a scale of 100, this multiplication ensures the value is represented correctly.
Q: Can all fractions be easily converted to percentages?
A: While all fractions can be converted to percentages, some may result in repeating or non-terminating decimals. In such cases, it may be necessary to round the percentage to a suitable number of decimal places.
Q: Is there a difference between percent and percentage?
A: "Percent" is used with a specific number (e.g., 60 percent), while "percentage" is a general term (e.g., "the percentage of students who passed"). They are often used interchangeably, but this distinction helps maintain clarity.
Q: What if the fraction is greater than 1?
A: If the fraction is greater than 1 (e.g., 3/2), the resulting percentage will be greater than 100%. For example, 3/2 = 1.5, and 1.5 × 100% = 150%.
Q: How can I improve my skills in converting fractions to percentages?
A: Practice is key. Work through various examples, focusing on understanding the underlying principles. Use online resources, textbooks, and worksheets to reinforce your knowledge.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill that is essential in various aspects of life. By understanding the basic principles and following the step-by-step methods outlined in this article, you can confidently convert any fraction to a percentage. Whether you are calculating test scores, analyzing sales discounts, or interpreting survey results, the ability to work with percentages is invaluable. Remember to avoid common mistakes, practice regularly, and apply your knowledge to real-world scenarios to master this skill. With a solid understanding of percentages, you’ll be well-equipped to make informed decisions and navigate the complexities of everyday life with greater ease and confidence. In the case of 12/20, we've shown that it equals 60%. Keep practicing and you'll become proficient in no time!
Latest Posts
Latest Posts
-
How Many Minutes Is 2 Hours
Dec 05, 2025
-
What Percentage Is 25 Of 500
Dec 05, 2025
-
Common Multiples Of 6 And 9
Dec 05, 2025
-
What Is 1 1 8 As A Decimal
Dec 05, 2025
-
What Is The Percent Of 12 20
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 12/20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.