What Is The 20 Of 200
bemquerermulher
Dec 05, 2025 · 8 min read
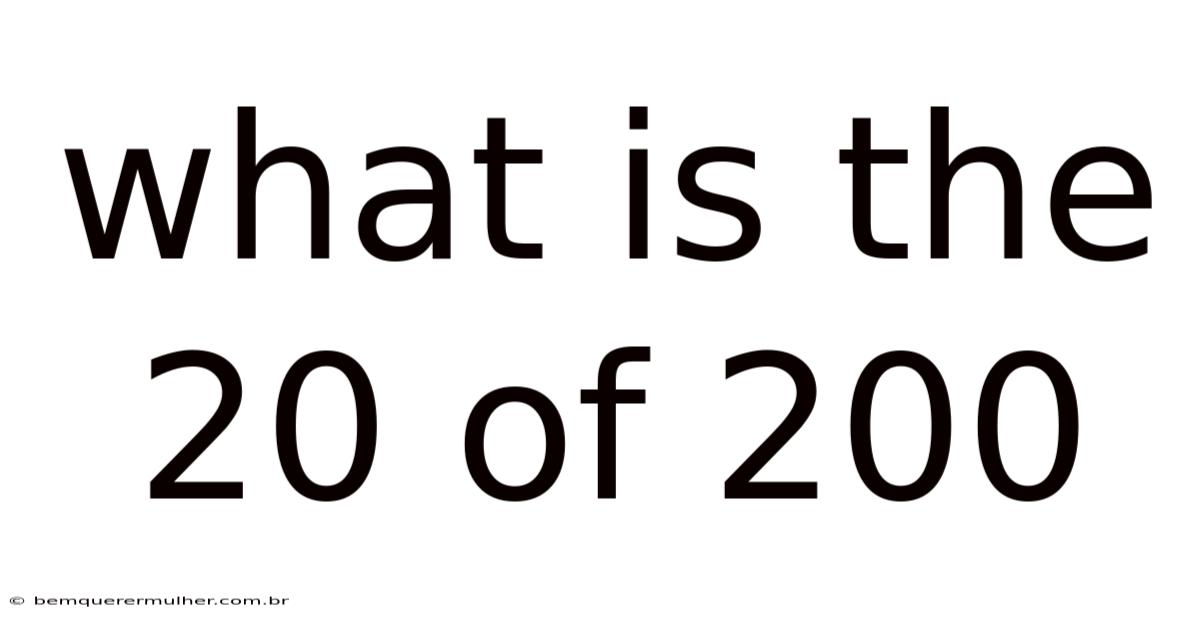
Table of Contents
Calculating "20% of 200" is a fundamental math skill with broad applications, from figuring out discounts while shopping to understanding financial reports. This article will break down the calculation process step-by-step, explore practical examples, and touch on the underlying mathematical principles to give you a solid understanding.
What Does "20% of 200" Mean?
To understand "20% of 200", let's clarify each component:
-
Percent (%): A percentage is a way of expressing a number as a fraction of 100. The "%" symbol means "out of 100" or "per 100." So, 20% means 20 out of every 100.
-
Of: In mathematics, "of" often indicates multiplication. So, "20% of 200" means 20% multiplied by 200.
-
200: This is the whole number or quantity from which we want to find a proportional part.
In essence, "20% of 200" asks: "What quantity represents twenty out of every hundred, taken from a total of 200?" Calculating this involves converting the percentage to a decimal or fraction and then multiplying it by the total amount.
How to Calculate 20% of 200: Step-by-Step
There are a couple of simple methods to calculate percentages. Here are the two most common:
Method 1: Converting the Percentage to a Decimal
This is a straightforward and widely used approach:
-
Convert the percentage to a decimal: Divide the percentage by 100.
- In our case, we have 20%. Thus, 20 / 100 = 0.20.
-
Multiply the decimal by the whole number: Multiply the decimal obtained in step 1 by the number you are taking the percentage of (in this case, 200).
- So, 0.20 * 200 = 40.
Therefore, 20% of 200 is 40.
Method 2: Converting the Percentage to a Fraction
This method is useful when you prefer working with fractions:
-
Convert the percentage to a fraction: Express the percentage as a fraction with a denominator of 100.
- Here, 20% becomes 20/100.
-
Simplify the fraction (optional): Simplifying the fraction can make the multiplication easier. 20/100 simplifies to 1/5.
-
Multiply the fraction by the whole number: Multiply the simplified fraction by the whole number (200).
- (1/5) * 200 = 200/5 = 40.
Again, we arrive at the conclusion that 20% of 200 is 40.
Why Does This Work? The Math Behind the Calculation
Understanding the underlying math can reinforce your understanding of percentage calculations:
-
Percentages as Proportions: A percentage represents a proportion or ratio. When we say "20% of 200," we're establishing a proportional relationship: 20 is to 100 as some unknown value (let's call it 'x') is to 200. This can be written as:
20 / 100 = x / 200
-
Solving for the Unknown: To find 'x', we cross-multiply:
20 * 200 = 100 * x
4000 = 100x
x = 4000 / 100
x = 40
This confirms that 20% of 200 is indeed 40.
-
Scaling: The concept is about scaling. We're essentially scaling down 200 by a factor represented by the percentage. When we convert 20% to 0.20, we are using a scale factor. Multiplying 200 by 0.20 gives us the scaled-down value, which is 40.
Real-World Examples
Percentages are all around us. Here are some situations where calculating "20% of 200" or similar calculations might be useful:
-
Discounts: Imagine an item originally priced at $200 is on sale with a 20% discount. To find the discount amount, you'd calculate 20% of 200. The discount is $40, so the sale price is $200 - $40 = $160.
-
Budgets: Suppose you allocate $200 for entertainment each month, and you want to set aside 20% of it for going to the movies. 20% of $200 is $40, which is the amount you'd budget for movies.
-
Tips: If your restaurant bill is $200 and you want to leave a 20% tip, you'd calculate 20% of $200. A 20% tip would be $40, making the total bill $240.
-
Taxes: In some scenarios, you might need to calculate taxes based on a percentage of an amount. For instance, if you owe 20% tax on a $200 purchase, the tax amount is $40.
-
Business: A store owner buys an item for $200 and wants to mark it up by 20%. The markup amount is 20% of $200, which is $40. The new selling price would be $240.
-
Data Analysis: In a dataset, you might find that out of 200 survey respondents, 20% chose a particular answer. Calculating 20% of 200 tells you that 40 people chose that specific response.
-
Investments: You invest $200 in a stock, and it increases in value by 20%. The increase in value is 20% of $200, which means your investment grew by $40.
Common Mistakes to Avoid
-
Forgetting to Convert the Percentage: The most frequent mistake is directly multiplying 20 by 200 without converting the percentage to a decimal or fraction. Remember, 20% is not the same as 20; it's 20 out of 100.
-
Misinterpreting "Of": Remember that "of" indicates multiplication. It's not addition, subtraction, or division.
-
Rounding Errors: If your calculations involve decimals, be careful with rounding. Rounding too early can lead to inaccuracies in the final result. It is best to keep as many decimal places as possible during the calculation and only round the final answer.
-
Using the Wrong Base Number: Make sure you're taking the percentage of the correct number. For instance, if you're calculating a discount, ensure you're taking the percentage of the original price, not a different number.
Advanced Applications of Percentages
Beyond simple calculations, percentages are crucial in various advanced contexts:
-
Financial Analysis: Percentages are used extensively in financial analysis to calculate growth rates, profit margins, and return on investments. Understanding percentage changes helps analysts assess a company's performance over time.
-
Statistics: In statistics, percentages are used to describe the distribution of data, calculate confidence intervals, and perform hypothesis testing. They provide a standardized way to compare data across different groups or samples.
-
Economics: Economists use percentages to analyze inflation rates, unemployment rates, and GDP growth. Percentage changes are essential indicators of economic health and stability.
-
Computer Science: Percentages are used in computer science for various purposes, such as calculating the accuracy of machine learning models, representing data compression ratios, and determining resource utilization in operating systems.
-
Project Management: Project managers use percentages to track project progress, allocate resources, and monitor budget expenditures. They provide a clear way to communicate project status to stakeholders.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The more you practice percentage calculations, the more comfortable and confident you'll become. Use real-life examples to reinforce your understanding.
-
Use Mental Math: Try to calculate simple percentages in your head. For example, calculating 10% of a number is as easy as moving the decimal point one place to the left.
-
Understand the Concepts: Don't just memorize formulas. Make sure you understand the underlying concepts and principles. This will help you apply percentages in various situations.
-
Use Technology: Take advantage of calculators and online tools to check your work and perform complex calculations. However, try to understand the manual process first.
-
Break Down Problems: When faced with a complex problem, break it down into smaller, more manageable steps. This will make the problem easier to solve.
FAQ About Calculating Percentages
-
How do I calculate the percentage increase or decrease?
- To calculate the percentage increase or decrease, use the formula: [((\text{New Value} - \text{Old Value}) / \text{Old Value}) * 100]
- For example, if a price increases from $100 to $120, the percentage increase is (((120 - 100) / 100) * 100 = 20%).
-
How do I find the original number if I know the percentage and the result?
- If you know that 20% of a number is 40, you can find the original number by dividing 40 by 0.20 (which is the decimal form of 20%).
- So, (40 / 0.20 = 200). The original number is 200.
-
Can percentages be greater than 100%?
- Yes, percentages can be greater than 100%. This typically occurs when comparing a new value to an original value and the new value is more than double the original. For example, if a company's revenue increases from $100,000 to $300,000, the percentage increase is (((300,000 - 100,000) / 100,000) * 100 = 200%).
-
How do I convert a fraction to a percentage?
- To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100.
- For example, to convert (\frac{3}{4}) to a percentage: (\frac{3}{4} = 0.75). Then, (0.75 * 100 = 75%).
-
How are percentages used in statistics?
- In statistics, percentages are used to express proportions and ratios, making it easier to understand and compare data. They are used in various applications, such as calculating confidence intervals, hypothesis testing, and analyzing survey results. For example, you might say that "60% of survey respondents agree with the statement."
Conclusion
Calculating "20% of 200" is not just a simple math problem; it's a foundational skill that permeates many aspects of daily life and professional fields. Whether you're calculating discounts, tipping at a restaurant, or analyzing financial data, understanding how to work with percentages is essential. By mastering the methods outlined in this article, avoiding common mistakes, and practicing regularly, you can confidently tackle percentage calculations in any situation.
Latest Posts
Latest Posts
-
How Many Feet Is 84 In
Dec 05, 2025
-
Wt Of One Gallon Of Water
Dec 05, 2025
-
What Is 61 Inches In Feet
Dec 05, 2025
-
How Many Inches In 3 Feet
Dec 05, 2025
-
What Is The 20 Of 200
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The 20 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.