What Is 7 Out Of 8 As A Percent
bemquerermulher
Dec 05, 2025 · 9 min read
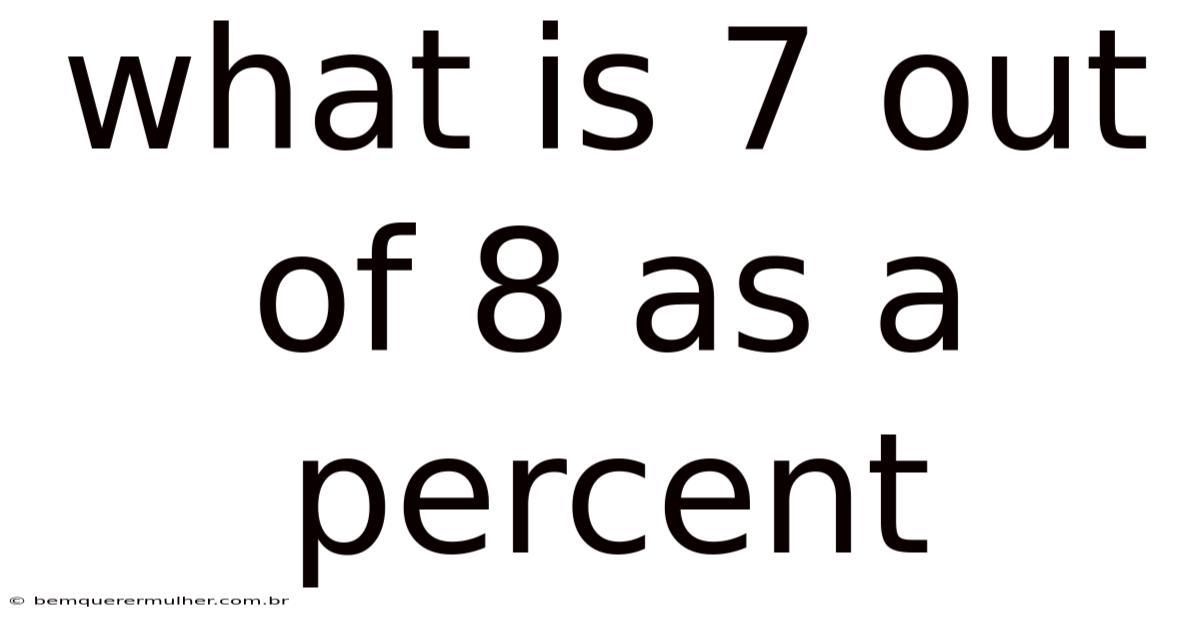
Table of Contents
Converting 7 out of 8 to a percentage is a straightforward process involving basic arithmetic. This article will explore the simple calculation needed to convert fractions to percentages and delve into the underlying concepts. It will also provide practical examples and address frequently asked questions to ensure a comprehensive understanding of the topic.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "per hundred." In essence, percentages provide a standardized way to compare different fractions and ratios. For instance, saying that 50% of a group of people prefer coffee means that 50 out of every 100 people in that group prefer coffee.
Percentages are used in various contexts, including finance, statistics, and everyday life, to represent proportions, changes, and rates. Understanding how to calculate and interpret percentages is a fundamental skill in mathematics and is crucial for making informed decisions in many situations.
The Basics of Fractions
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts of the whole are being considered, while the denominator indicates the total number of equal parts that make up the whole.
In the fraction 7/8:
- 7 is the numerator, representing the number of parts we are interested in.
- 8 is the denominator, representing the total number of parts in the whole.
Fractions can be converted to decimals and percentages, providing different ways to express the same proportion. Understanding fractions is essential for grasping the concept of percentages, as percentages are essentially fractions with a denominator of 100.
Converting 7/8 to a Percentage: Step-by-Step
Converting 7/8 to a percentage involves a simple two-step process:
- Convert the fraction to a decimal: Divide the numerator (7) by the denominator (8).
- Convert the decimal to a percentage: Multiply the decimal by 100.
Let's go through each step in detail.
Step 1: Convert the Fraction to a Decimal
To convert the fraction 7/8 to a decimal, divide 7 by 8:
7 ÷ 8 = 0.875
So, the decimal equivalent of 7/8 is 0.875.
Step 2: Convert the Decimal to a Percentage
To convert the decimal 0.875 to a percentage, multiply it by 100:
- 875 × 100 = 87.5
Therefore, 7/8 is equal to 87.5%.
Detailed Calculation
To reiterate, here’s the detailed calculation:
- Fraction: 7/8
- Decimal Conversion:
- Divide 7 by 8:
- 7 ÷ 8 = 0.875
- Percentage Conversion:
- Multiply the decimal by 100:
- 0.875 × 100 = 87.5%
Thus, 7 out of 8 as a percentage is 87.5%.
Practical Examples of Using Percentages
Understanding percentages is valuable in various real-world scenarios. Here are a few examples:
Example 1: Test Scores
Suppose you scored 7 out of 8 on a quiz. To find your percentage score:
- Convert the fraction 7/8 to a percentage: 87.5%.
- This means you scored 87.5% on the quiz.
Example 2: Sales Discount
If a store advertises that 7 out of 8 items are on sale, it means:
- 87.5% of the items are discounted.
Example 3: Survey Results
In a survey, if 7 out of 8 people prefer a certain product, it means:
- 87.5% of the people surveyed prefer that product.
Why is Understanding Percentage Conversion Important?
Understanding how to convert fractions to percentages is essential for several reasons:
- Comparison: Percentages provide a standardized way to compare proportions. It’s easier to compare 87.5% to other percentages than to compare the fraction 7/8 to other fractions.
- Decision Making: Percentages are used in finance to understand interest rates, investment returns, and loan terms. They help in making informed financial decisions.
- Data Analysis: In statistics, percentages are used to analyze and interpret data. They provide a clear way to present findings and draw conclusions.
- Everyday Life: From calculating discounts while shopping to understanding nutritional information on food labels, percentages are used in numerous everyday situations.
Common Mistakes to Avoid
When converting fractions to percentages, there are a few common mistakes to avoid:
- Incorrect Division: Ensure you divide the numerator by the denominator correctly. Recheck your calculation to avoid errors.
- Forgetting to Multiply by 100: After converting the fraction to a decimal, remember to multiply by 100 to express it as a percentage.
- Misinterpreting the Result: Understand what the percentage represents in the given context. For example, 87.5% could represent a test score, a discount rate, or a proportion in a survey.
Alternative Methods for Converting Fractions to Percentages
While the standard method involves converting the fraction to a decimal and then to a percentage, there are alternative methods you can use:
Method 1: Direct Multiplication
If possible, try to multiply the denominator by a number that results in 100. Then, multiply the numerator by the same number. This will give you a fraction with a denominator of 100, which is easily converted to a percentage.
For 7/8, it's not straightforward to multiply 8 by a whole number to get 100. However, this method works well for fractions like 1/4 (multiply both numerator and denominator by 25 to get 25/100 = 25%).
Method 2: Using Proportions
Set up a proportion where the fraction is equal to a percentage over 100. For example:
7/8 = x/100
To solve for x, cross-multiply:
8x = 7 * 100
8x = 700
x = 700 / 8
x = 87.5
So, 7/8 = 87.5/100, which means 7/8 is 87.5%.
The Scientific Explanation
The conversion of a fraction to a percentage is based on the fundamental principles of mathematics. A fraction represents a part of a whole, and a percentage expresses this part as a proportion of 100. The conversion process involves scaling the fraction to have a denominator of 100, which allows for easy comparison and interpretation.
The decimal equivalent of a fraction is obtained by dividing the numerator by the denominator. This decimal represents the same proportion as the fraction but in a different form. Multiplying the decimal by 100 scales it to represent the number of parts out of 100, which is the definition of a percentage.
Mathematically, this can be represented as:
Percentage = (Numerator / Denominator) × 100
In the case of 7/8:
Percentage = (7 / 8) × 100
Percentage = 0.875 × 100
Percentage = 87.5%
This scientific explanation highlights the logical and mathematical basis for converting fractions to percentages, emphasizing the underlying principles of proportion and scaling.
Examples of Other Fraction to Percentage Conversions
To further illustrate the process, here are a few more examples of converting fractions to percentages:
Example 1: 1/2
- Convert to decimal: 1 ÷ 2 = 0.5
- Convert to percentage: 0.5 × 100 = 50%
- So, 1/2 is 50%.
Example 2: 1/4
- Convert to decimal: 1 ÷ 4 = 0.25
- Convert to percentage: 0.25 × 100 = 25%
- So, 1/4 is 25%.
Example 3: 3/4
- Convert to decimal: 3 ÷ 4 = 0.75
- Convert to percentage: 0.75 × 100 = 75%
- So, 3/4 is 75%.
Example 4: 1/5
- Convert to decimal: 1 ÷ 5 = 0.2
- Convert to percentage: 0.2 × 100 = 20%
- So, 1/5 is 20%.
Example 5: 3/5
- Convert to decimal: 3 ÷ 5 = 0.6
- Convert to percentage: 0.6 × 100 = 60%
- So, 3/5 is 60%.
Advanced Applications of Percentages
Beyond basic conversions, percentages are used in more complex calculations and analyses. Here are a few advanced applications:
Calculating Percentage Change
Percentage change is used to describe the relative difference between two values. The formula for percentage change is:
Percentage Change = [(New Value - Old Value) / Old Value] × 100
For example, if a stock price increases from $50 to $60, the percentage change is:
Percentage Change = [($60 - $50) / $50] × 100 = (10 / 50) × 100 = 20%
Calculating Percentage Increase and Decrease
Percentage increase and decrease are specific types of percentage change. If the new value is greater than the old value, it's a percentage increase. If the new value is less than the old value, it's a percentage decrease.
Calculating Compound Interest
Compound interest is calculated on the initial principal and also on the accumulated interest of previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Percentages are used to express the interest rate (r) in this formula.
Statistical Analysis
In statistics, percentages are used to represent proportions, probabilities, and confidence intervals. They are essential for interpreting data and drawing meaningful conclusions.
FAQ About Converting Fractions to Percentages
Here are some frequently asked questions about converting fractions to percentages:
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator to get a decimal, then multiply the decimal by 100.
Q: Why do I need to multiply by 100?
A: Multiplying by 100 converts the decimal to a percentage, which is a proportion out of 100.
Q: Can all fractions be converted to percentages?
A: Yes, all fractions can be converted to percentages using the method described.
Q: What is the percentage equivalent of 1?
A: The percentage equivalent of 1 is 100%.
Q: How do I convert a mixed number to a percentage?
A: First, convert the mixed number to an improper fraction, then follow the same steps as converting a regular fraction to a percentage.
Q: Is there a shortcut for converting common fractions to percentages?
A: Yes, knowing the percentage equivalents of common fractions like 1/2 (50%), 1/4 (25%), and 3/4 (75%) can save time.
Conclusion
Converting 7 out of 8 to a percentage is a fundamental mathematical skill with practical applications in various aspects of life. By following the simple steps of converting the fraction to a decimal and then multiplying by 100, you can easily find that 7/8 is equal to 87.5%. Understanding percentages allows for easy comparison, informed decision-making, and effective data analysis. Whether it's calculating test scores, understanding discounts, or interpreting survey results, mastering percentage conversions is an invaluable tool. Avoiding common mistakes and exploring alternative methods can further enhance your understanding and proficiency in using percentages.
Latest Posts
Latest Posts
-
What Is 15 50 As A Percent
Dec 05, 2025
-
How Many Inches Is 16 Feet
Dec 05, 2025
-
How Many Feet Are In 55 Inches
Dec 05, 2025
-
What Cell Type Is A Bald Eagle
Dec 05, 2025
-
What Is 7 Out Of 8 As A Percent
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 7 Out Of 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.