What Is 25/100 As A Percent
bemquerermulher
Dec 04, 2025 · 8 min read
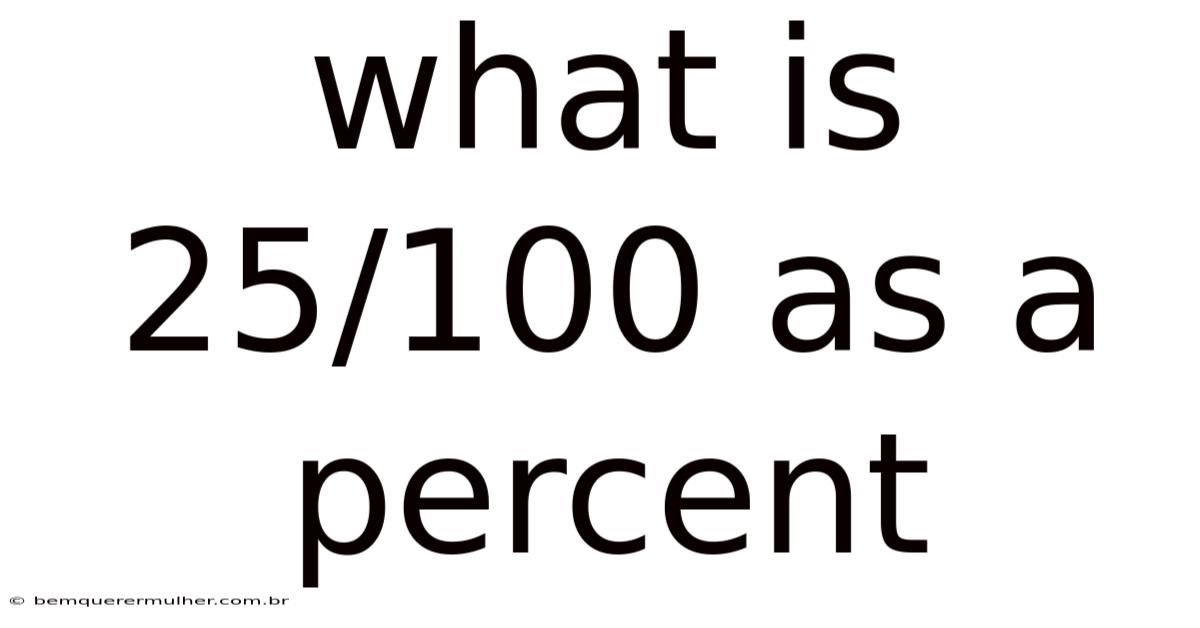
Table of Contents
Converting 25/100 to a percentage is a fundamental concept in mathematics that bridges fractions and percentages, offering a clear way to understand proportions and ratios in various contexts. This conversion is particularly useful in everyday situations, such as calculating discounts, understanding financial data, or interpreting statistical information. By expressing 25/100 as a percentage, we transform it into a more universally understandable format, where the fraction is represented as a part of 100, making comparisons and interpretations straightforward. This article will explore the concept, its importance, and provide a step-by-step guide to perform the conversion, enhancing your mathematical literacy and practical skills.
Understanding Fractions and Percentages
Fractions and percentages are two different ways of representing parts of a whole. Understanding their relationship is crucial for various mathematical applications.
What is a Fraction? A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number).
- The numerator indicates how many parts of the whole you have.
- The denominator indicates the total number of equal parts that make up the whole.
For example, in the fraction 25/100:
- 25 is the numerator, representing the number of parts you have.
- 100 is the denominator, representing the total number of parts.
What is a Percentage? A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," which means "out of one hundred." Percentages are denoted by the symbol %.
- For example, 25% means 25 out of 100.
- Percentages make it easier to compare different proportions because they all relate to the same base (100).
The Relationship Between Fractions and Percentages
The connection between fractions and percentages is that a percentage is essentially a fraction with a denominator of 100. Converting a fraction to a percentage involves scaling the fraction so that its denominator becomes 100. If the fraction already has a denominator of 100, then the numerator directly represents the percentage.
- Fraction to Percentage: To convert a fraction to a percentage, you can multiply the fraction by 100%.
- Percentage to Fraction: To convert a percentage to a fraction, you divide the percentage by 100 and simplify.
Why Convert Fractions to Percentages?
Converting fractions to percentages is a fundamental skill with numerous practical applications. Here are some key reasons why this conversion is important:
- Easy Comparison: Percentages provide a standardized way to compare different proportions. It's much easier to compare 25% and 50% than to compare fractions like 1/4 and 1/2.
- Real-World Applications: Percentages are used extensively in everyday life, including:
- Finance: Calculating interest rates, discounts, and investment returns.
- Retail: Determining sale prices and markups.
- Statistics: Representing data and survey results.
- Education: Grading and assessing performance.
- Clear Communication: Percentages are easily understood by a wide audience, making them useful for communicating information clearly and effectively.
- Problem Solving: Converting fractions to percentages simplifies many mathematical problems, allowing for easier calculations and interpretations.
Step-by-Step Guide: Converting 25/100 to a Percentage
Converting the fraction 25/100 to a percentage is straightforward because the denominator is already 100. Here’s a detailed step-by-step guide:
Step 1: Understand the Fraction The fraction 25/100 means "25 parts out of 100." The numerator is 25, and the denominator is 100.
Step 2: Recognize the Denominator Since the denominator is already 100, the fraction is already in the form of a percentage. This simplifies the conversion process significantly.
Step 3: Convert to Percentage To convert a fraction to a percentage, you multiply the fraction by 100%. In this case, the fraction is 25/100.
(25/100) * 100%
Step 4: Perform the Calculation Multiply the fraction by 100%.
(25/100) * 100% = (25 * 100) / 100 %
Step 5: Simplify the Expression Simplify the expression by dividing 25 * 100 by 100.
(25 * 100) / 100 % = 2500 / 100 %
2500 / 100 % = 25%
Step 6: State the Result The result of converting 25/100 to a percentage is 25%.
Alternative Method: Direct Observation
When the fraction has a denominator of 100, the numerator directly represents the percentage. Therefore, 25/100 is simply 25%.
Examples of Converting Other Fractions to Percentages
To further illustrate the concept, let's look at a few additional examples of converting fractions to percentages:
Example 1: Convert 1/2 to a Percentage
- Fraction: 1/2
- Multiply by 100%: (1/2) * 100%
- Calculate: (1 * 100) / 2 % = 100 / 2 %
- Simplify: 100 / 2 % = 50%
- Result: 1/2 = 50%
Example 2: Convert 3/4 to a Percentage
- Fraction: 3/4
- Multiply by 100%: (3/4) * 100%
- Calculate: (3 * 100) / 4 % = 300 / 4 %
- Simplify: 300 / 4 % = 75%
- Result: 3/4 = 75%
Example 3: Convert 1/5 to a Percentage
- Fraction: 1/5
- Multiply by 100%: (1/5) * 100%
- Calculate: (1 * 100) / 5 % = 100 / 5 %
- Simplify: 100 / 5 % = 20%
- Result: 1/5 = 20%
Practical Applications of Percentages
1. Finance Percentages are commonly used in finance to express interest rates, returns on investments, and changes in stock prices.
- Interest Rates: If you deposit money in a savings account with an annual interest rate of 5%, this means that for every $100 you deposit, you will earn $5 in interest over the course of a year.
- Investment Returns: If an investment increases in value by 15%, it means that for every $100 you invested, you have earned $15.
2. Retail Retailers use percentages to calculate discounts, markups, and profit margins.
- Discounts: A 20% discount on an item means that the price is reduced by 20% of the original price. For example, if an item originally costs $50, a 20% discount reduces the price by $10 (20% of $50), making the final price $40.
- Markups: A markup of 50% on a product means that the selling price is 50% higher than the cost price. If a store buys an item for $20 and marks it up by 50%, the selling price will be $30.
3. Statistics Percentages are used to represent data in a way that is easy to understand and compare.
- Survey Results: If a survey finds that 60% of respondents prefer a certain product, it means that out of every 100 people surveyed, 60 prefer that product.
- Demographics: Percentages are used to describe the composition of populations, such as the percentage of people in a certain age group or the percentage of households with children.
4. Education Percentages are used to calculate grades and assess student performance.
- Grading: If a student scores 85 out of 100 on a test, their grade is 85%.
- Performance Metrics: Percentages can be used to track student progress and compare performance across different groups.
Common Mistakes to Avoid
When working with fractions and percentages, it's important to avoid common mistakes that can lead to incorrect results. Here are some common pitfalls to watch out for:
- Misunderstanding the Base: Always be clear about what the percentage is "of." For example, a 10% increase followed by a 10% decrease does not result in the original amount because the base changes after the first operation.
- Incorrect Conversion: Ensure that you are correctly multiplying or dividing by 100 when converting between fractions and percentages.
- Ignoring Simplification: Always simplify fractions to their lowest terms before converting to a percentage, if possible. This can make the calculation easier and reduce errors.
- Confusing Percentage Points with Percentages: Understand the difference between a percentage increase and a percentage point increase. For example, if an interest rate increases from 5% to 7%, it has increased by 2 percentage points, but the percentage increase is 40% (2/5 * 100%).
Advanced Concepts: Percentage Change
Understanding percentage change is crucial in many applications, particularly in finance and economics. Percentage change is the extent to which a variable gains or loses value. It is calculated as:
Percentage Change = [(New Value - Old Value) / Old Value] * 100%
- Example: If a stock price increases from $50 to $60, the percentage change is:
Percentage Change = [($60 - $50) / $50] * 100% = ($10 / $50) * 100% = 0.2 * 100% = 20%
This means the stock price has increased by 20%.
Tips for Mastering Percentage Calculations
To become proficient with percentage calculations, consider the following tips:
- Practice Regularly: The more you practice, the more comfortable you will become with converting fractions to percentages and solving percentage-related problems.
- Use Real-World Examples: Apply percentages to real-world scenarios to understand their practical applications.
- Understand the Fundamentals: Make sure you have a solid understanding of fractions, decimals, and the basic principles of percentage calculations.
- Use Online Tools: Utilize online calculators and resources to check your work and explore different percentage-related concepts.
- Break Down Complex Problems: When faced with a complex problem, break it down into smaller, more manageable steps.
Conclusion
Converting the fraction 25/100 to a percentage is a straightforward process that yields 25%. This conversion is a fundamental skill with wide-ranging applications in finance, retail, statistics, and education. By understanding the relationship between fractions and percentages, and by following the step-by-step guide outlined in this article, you can confidently convert fractions to percentages and apply this knowledge to solve real-world problems. Consistent practice and a solid understanding of the underlying concepts will further enhance your proficiency with percentage calculations, making you more adept at interpreting and using numerical information in various contexts. Remember to avoid common mistakes, such as misunderstanding the base and confusing percentage points with percentages, to ensure accurate results. With these skills, you can effectively analyze and communicate quantitative data, empowering you in both your personal and professional life.
Latest Posts
Latest Posts
-
What Was The Time 9 Hours Ago
Dec 04, 2025
-
How Many Ounces In A Quarter Pound
Dec 04, 2025
-
How Many Grams In A 1 4 Of An Ounce
Dec 04, 2025
-
What Is 25 100 As A Percent
Dec 04, 2025
-
What Is A 25 Out Of 30
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 25/100 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.