9 Out Of 12 As A Percentage
bemquerermulher
Dec 04, 2025 · 7 min read
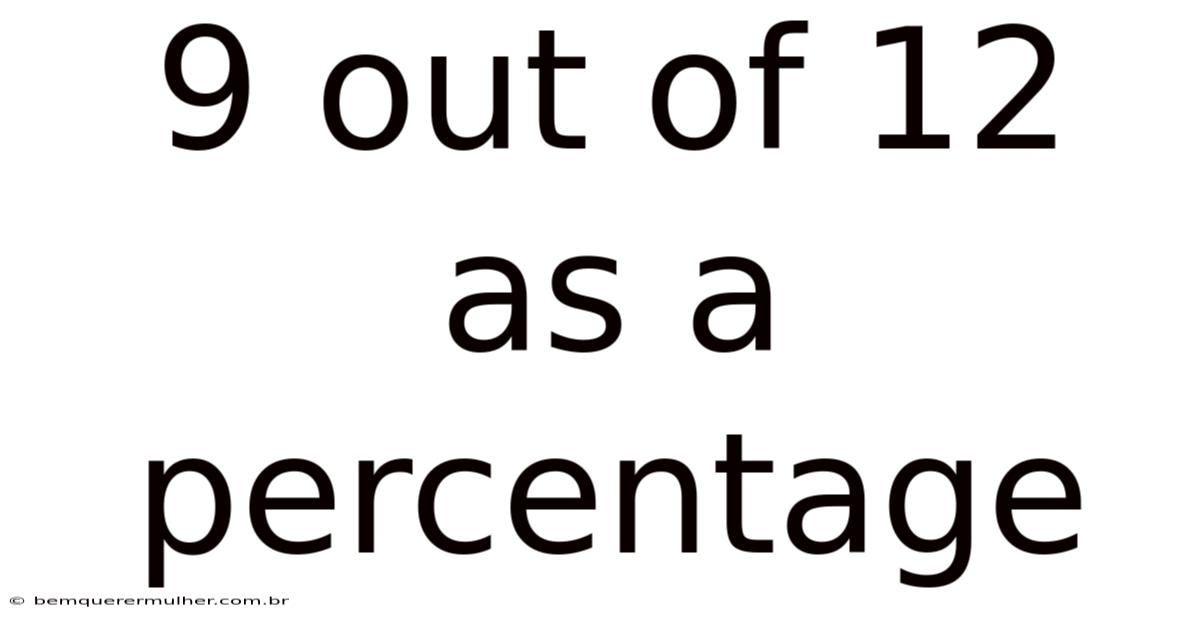
Table of Contents
Calculating "9 out of 12" as a percentage is a fundamental math skill with widespread applications, from grading papers to figuring out discounts. Understanding how to convert fractions into percentages not only strengthens your numerical literacy but also provides a practical tool for everyday problem-solving. In this article, we will explore step-by-step methods to easily convert 9/12 to a percentage, understand its real-world applications, and delve into the underlying mathematical principles.
Understanding Percentages
Percentage comes from the Latin per centum, meaning "out of one hundred." A percentage is a way of expressing a number as a fraction of 100. It is a dimensionless number (pure number) and has no standard unit of measurement.
Importance of Understanding Percentages
- Daily Life: Percentages are used to calculate discounts, sales tax, and tips.
- Finance: Interest rates, investment returns, and inflation rates are all expressed as percentages.
- Statistics: Understanding percentages is essential for interpreting statistical data, such as survey results and demographic information.
- Education: Grades are often given as percentages, which help to quickly understand performance relative to the total possible score.
Converting Fractions to Percentages: The Basics
To convert a fraction to a percentage, you generally follow two steps:
- Divide the Numerator by the Denominator: This converts the fraction into a decimal.
- Multiply by 100: This converts the decimal into a percentage.
Formula for Converting a Fraction to a Percentage
The formula to convert a fraction (\frac{a}{b}) to a percentage is:
[ \text{Percentage} = \left( \frac{a}{b} \right) \times 100 ]
Step-by-Step Guide: Converting 9 out of 12 to a Percentage
Let's apply the basic principles to convert the fraction (\frac{9}{12}) to a percentage.
Step 1: Divide the Numerator by the Denominator
First, divide 9 by 12:
[ \frac{9}{12} = 0.75 ]
Step 2: Multiply by 100
Next, multiply the result by 100:
[ 0.75 \times 100 = 75% ]
Therefore, 9 out of 12 as a percentage is (75%).
Alternative Method: Simplifying the Fraction First
Simplifying the fraction before converting it to a percentage can sometimes make the calculation easier.
Step 1: Simplify the Fraction
The fraction (\frac{9}{12}) can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 3.
[ \frac{9 \div 3}{12 \div 3} = \frac{3}{4} ]
Step 2: Convert the Simplified Fraction to a Percentage
Now, convert (\frac{3}{4}) to a percentage:
- Divide the numerator by the denominator: [ \frac{3}{4} = 0.75 ]
- Multiply by 100: [ 0.75 \times 100 = 75% ]
Using this method, we also find that 9 out of 12 is equal to (75%).
Real-World Applications
Understanding how to calculate percentages is valuable in numerous real-world scenarios. Here are a few examples:
1. Calculating Grades
Suppose a student scores 9 out of 12 on a quiz. To find the student's grade as a percentage:
[ \text{Grade Percentage} = \left( \frac{9}{12} \right) \times 100 = 75% ]
This means the student scored 75% on the quiz.
2. Determining Discounts
If an item originally priced at $40 is on sale for $10 off, you want to know what percentage discount you’re receiving. First, calculate the fraction of the discount:
[ \frac{\text{Discount}}{\text{Original Price}} = \frac{10}{40} = \frac{1}{4} = 0.25 ]
Then, convert this to a percentage:
[ 0.25 \times 100 = 25% ]
So, the item is 25% off.
3. Calculating Proportions
In a survey, if 9 out of 12 people prefer coffee over tea, this can be expressed as a percentage:
[ \text{Percentage} = \left( \frac{9}{12} \right) \times 100 = 75% ]
This indicates that 75% of the people surveyed prefer coffee.
4. Analyzing Sales Data
A business finds that 9 out of every 12 customers who visit their store make a purchase. To understand their conversion rate:
[ \text{Conversion Rate} = \left( \frac{9}{12} \right) \times 100 = 75% ]
The store has a 75% conversion rate.
Common Mistakes to Avoid
When converting fractions to percentages, be aware of these common pitfalls:
- Incorrect Division: Ensure you divide the numerator by the denominator correctly. A mistake here will skew the final percentage.
- Forgetting to Multiply by 100: Failing to multiply the decimal by 100 will give you a decimal result instead of a percentage.
- Misinterpreting the Fraction: Make sure you understand which number is the numerator and which is the denominator. Mixing them up will lead to an incorrect percentage.
- Rounding Errors: If the decimal repeats, round to an appropriate number of decimal places before multiplying by 100 to maintain accuracy.
Advanced Applications of Percentages
Beyond basic calculations, percentages are used in more complex scenarios such as:
1. Compound Interest
Understanding percentages is crucial for calculating compound interest, which is interest calculated on the initial principal and also on the accumulated interest of previous periods.
2. Statistical Analysis
In statistics, percentages are used to describe data sets, calculate confidence intervals, and perform hypothesis testing.
3. Financial Modeling
Financial models often use percentages to forecast growth rates, calculate returns on investment, and assess risk.
4. Project Management
Project managers use percentages to track project progress, allocate resources, and monitor budget expenditures.
Practice Questions
To solidify your understanding, try these practice questions:
- What is 6 out of 8 as a percentage?
- Convert (\frac{15}{20}) to a percentage.
- If you scored 21 out of 25 on a test, what is your percentage score?
- What percentage is 18 out of 24?
- Convert (\frac{5}{8}) to a percentage.
Answers
- 75%
- 75%
- 84%
- 75%
- 62.5%
Deep Dive into Percentage Calculations
To fully grasp the concept of percentages, let's explore additional scenarios and techniques.
Calculating Percentage Increase and Decrease
Percentage increase and decrease are used to find the change in a quantity relative to its original value.
Percentage Increase Formula:
[ \text{Percentage Increase} = \left( \frac{\text{New Value} - \text{Original Value}}{\text{Original Value}} \right) \times 100 ]
Percentage Decrease Formula:
[ \text{Percentage Decrease} = \left( \frac{\text{Original Value} - \text{New Value}}{\text{Original Value}} \right) \times 100 ]
Example of Percentage Increase:
If a price increases from $50 to $60:
[ \text{Percentage Increase} = \left( \frac{60 - 50}{50} \right) \times 100 = \left( \frac{10}{50} \right) \times 100 = 20% ]
There is a 20% increase in price.
Example of Percentage Decrease:
If a price decreases from $50 to $40:
[ \text{Percentage Decrease} = \left( \frac{50 - 40}{50} \right) \times 100 = \left( \frac{10}{50} \right) \times 100 = 20% ]
There is a 20% decrease in price.
Working Backwards: Finding the Original Value
Sometimes, you may need to find the original value when you know the percentage and the new value.
Formula to Find the Original Value after a Percentage Increase:
[ \text{Original Value} = \frac{\text{New Value}}{1 + \frac{\text{Percentage Increase}}{100}} ]
Formula to Find the Original Value after a Percentage Decrease:
[ \text{Original Value} = \frac{\text{New Value}}{1 - \frac{\text{Percentage Decrease}}{100}} ]
Example:
After a 10% increase, the price of an item is $110. What was the original price?
[ \text{Original Value} = \frac{110}{1 + \frac{10}{100}} = \frac{110}{1.1} = $100 ]
The original price was $100.
Percentages in Different Fields
1. Business and Finance
In business, percentages are used to calculate profit margins, revenue growth, and market share. Financial analysts use percentages to evaluate investment performance and assess risk.
2. Healthcare
In healthcare, percentages are used to report survival rates, calculate medication dosages, and track disease prevalence.
3. Retail
Retailers use percentages to calculate discounts, markups, and sales tax. They also use percentages to analyze sales trends and manage inventory.
4. Education
Educators use percentages to grade assignments, assess student performance, and track academic progress.
5. Technology
In technology, percentages are used to measure system performance, calculate error rates, and analyze data.
Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice, the more comfortable you will become with percentage calculations.
- Use Real-World Examples: Apply percentages to everyday situations to reinforce your understanding.
- Understand the Formulas: Knowing the formulas will help you solve more complex problems.
- Check Your Work: Always double-check your calculations to avoid errors.
- Use Tools Wisely: Calculators and online tools can be helpful, but make sure you understand the underlying concepts.
Conclusion
Converting 9 out of 12 to a percentage is a straightforward process that involves dividing the numerator by the denominator and then multiplying by 100. This fundamental skill is essential for various real-world applications, including calculating grades, determining discounts, and analyzing data. By understanding the basic principles and practicing regularly, you can master percentage calculations and apply them effectively in your daily life. Remember to simplify fractions when possible and always double-check your work to ensure accuracy. Percentages are not just numbers; they are powerful tools for understanding and interpreting the world around us.
Latest Posts
Latest Posts
-
How Many Cups Is 15 Ounces
Dec 04, 2025
-
How Many Minutes Is 12 Hours
Dec 04, 2025
-
9 Out Of 12 As A Percentage
Dec 04, 2025
-
How Tall Is 60 Inches In Feet
Dec 04, 2025
-
How Many Oz In 6 Cups
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.