30 Of 200 Is What Percent
bemquerermulher
Dec 06, 2025 · 8 min read
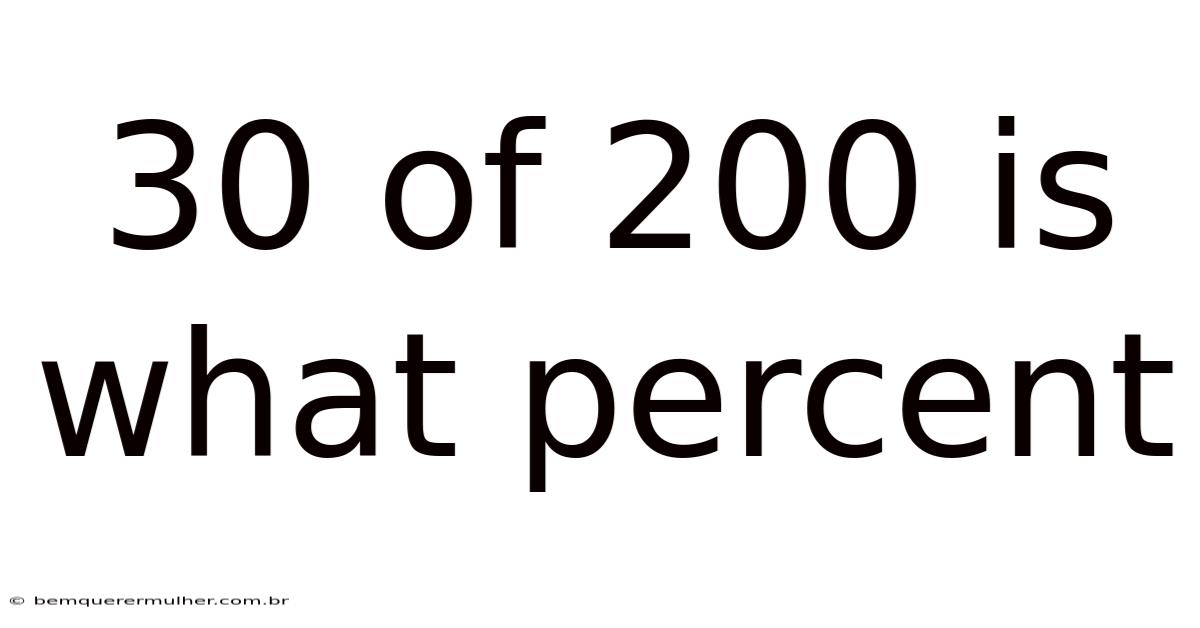
Table of Contents
Calculating percentages is a fundamental skill in mathematics and is essential for understanding various real-life situations, from calculating discounts while shopping to interpreting statistical data. The question "30 of 200 is what percent?" is a basic percentage problem that can be easily solved with a clear understanding of the underlying principles. In this article, we will explore in detail how to calculate this percentage, provide practical examples, and discuss the importance of understanding percentages in everyday life.
Understanding Percentages
Percentage means "per hundred" or "out of 100." It is a way of expressing a number as a fraction of 100. The symbol "%" is used to denote percentage. For example, 50% means 50 out of 100, which is equivalent to one-half.
Basic Formula for Percentage
The basic formula to calculate percentage is: $\text{Percentage} = \left( \frac{\text{Part}}{\text{Whole}} \right) \times 100$ Here:
- Part is the specific quantity you are interested in.
- Whole is the total quantity.
How to Calculate "30 of 200 is What Percent?"
To find out what percent 30 is of 200, we can use the percentage formula mentioned above.
Step-by-Step Calculation
-
Identify the Part and the Whole:
- In this case, the Part is 30.
- The Whole is 200.
-
Apply the Percentage Formula: $\text{Percentage} = \left( \frac{30}{200} \right) \times 100$
-
Simplify the Fraction: $\frac{30}{200} = \frac{3}{20}$
-
Multiply by 100: $\text{Percentage} = \frac{3}{20} \times 100$
-
Calculate the Percentage: $\text{Percentage} = 3 \times 5 = 15$ So, 30 is 15% of 200.
Alternative Method: Using Decimal Conversion
Another way to calculate the percentage is by converting the fraction to a decimal first and then multiplying by 100.
-
Convert the Fraction to a Decimal: $\frac{30}{200} = 0.15$
-
Multiply by 100: $\text{Percentage} = 0.15 \times 100 = 15%$ Again, this method confirms that 30 is 15% of 200.
Practical Examples of Percentage Calculations
To further illustrate the concept, let's look at some practical examples where percentage calculations are used.
Example 1: Calculating Test Scores
Suppose a student scores 30 out of 200 on a test. What percentage did the student score?
- Part = 30 (marks obtained)
- Whole = 200 (total marks) $\text{Percentage} = \left( \frac{30}{200} \right) \times 100 = 15%$ The student scored 15% on the test.
Example 2: Determining the Percentage of Savings
Imagine you saved $30 out of a total income of $200. What percentage of your income did you save?
- Part = $30 (savings)
- Whole = $200 (total income) $\text{Percentage} = \left( \frac{30}{200} \right) \times 100 = 15%$ You saved 15% of your income.
Example 3: Calculating Discount Percentage
A store offers a discount of $30 on an item originally priced at $200. What is the discount percentage?
- Part = $30 (discount amount)
- Whole = $200 (original price) $\text{Percentage} = \left( \frac{30}{200} \right) \times 100 = 15%$ The discount is 15% of the original price.
Importance of Understanding Percentages
Understanding percentages is crucial for various reasons. Here are some key areas where percentages play a significant role:
1. Financial Literacy
Percentages are extensively used in finance. Whether it's calculating interest rates on loans, understanding investment returns, or determining discounts while shopping, percentages are indispensable.
- Interest Rates: Interest rates on loans and savings accounts are expressed as percentages. Knowing how to calculate these percentages helps in understanding the actual cost of borrowing or the actual return on investment.
- Discounts and Sales: Retailers often use percentages to indicate discounts. For example, a "20% off" sale means you save 20% of the original price.
- Budgeting: Percentages help in creating and managing budgets. For instance, you might allocate 30% of your income to housing, 20% to food, and so on.
2. Academic Performance
In academics, percentages are used to evaluate performance in tests, exams, and assignments. Understanding how percentages are calculated helps students gauge their progress and set realistic goals.
- Grading Systems: Many educational institutions use percentages to represent grades. A score of 80% might be a "B," while 90% or higher might be an "A."
- Progress Tracking: Students can track their academic progress by monitoring their percentage scores over time.
3. Data Interpretation
Percentages are commonly used in statistical data to make comparisons and draw conclusions. Being able to interpret percentages is essential in fields like market research, economics, and social sciences.
- Surveys and Polls: Survey results are often presented in percentages. For example, a poll might show that 60% of respondents support a particular policy.
- Market Share: Companies often use percentages to describe their market share. For instance, a company might have 35% of the market share in a particular industry.
4. Health and Nutrition
Percentages are used to understand nutritional information, calculate body fat percentage, and monitor health indicators.
- Nutritional Labels: Food labels often list the percentage of daily values for various nutrients. This helps consumers make informed choices about their diet.
- Body Fat Percentage: Health professionals use body fat percentage to assess an individual's fitness and health.
5. Everyday Decision Making
In everyday life, percentages help in making informed decisions, whether it's calculating tips at restaurants, understanding probabilities, or comparing prices.
- Tipping: When dining out, calculating a 15% or 20% tip is a common practice.
- Probability: Percentages are used to express the likelihood of events. For example, "there is a 30% chance of rain."
- Price Comparison: When shopping, comparing prices based on percentage discounts can help in finding the best deals.
Common Mistakes to Avoid When Calculating Percentages
While calculating percentages is straightforward, there are some common mistakes that people often make. Here are some to watch out for:
1. Confusing the Part and the Whole
One of the most common mistakes is confusing which number is the part and which is the whole. Always ensure that you correctly identify the base number (the whole) and the specific quantity you're interested in (the part).
- Example: If the question is "What percent of 50 is 10?", make sure you understand that 50 is the whole and 10 is the part.
2. Forgetting to Multiply by 100
After dividing the part by the whole, remember to multiply the result by 100 to express it as a percentage. Forgetting this step will give you the decimal form, not the percentage.
- Example: If you calculate $\frac{15}{100} = 0.15$, remember to multiply by 100 to get 15%.
3. Incorrectly Simplifying Fractions
When simplifying fractions, ensure that you divide both the numerator and the denominator by the same number. Incorrect simplification can lead to wrong answers.
- Example: If you have $\frac{30}{200}$, correctly simplify it to $\frac{3}{20}$ by dividing both numbers by 10.
4. Misinterpreting Percentage Increase or Decrease
When calculating percentage increase or decrease, make sure you use the correct formula: $\text{Percentage Change} = \left( \frac{\text{New Value} - \text{Old Value}}{\text{Old Value}} \right) \times 100$ Using the wrong formula or misinterpreting the values can lead to incorrect results.
- Example: If a price increases from $100 to $120, the percentage increase is: $\left( \frac{120 - 100}{100} \right) \times 100 = 20%$
5. Not Double-Checking the Answer
Always double-check your answer to ensure it makes sense in the context of the problem. If the percentage seems unusually high or low, review your calculations to identify any errors.
- Example: If you're calculating a discount and the percentage seems too high, double-check that you've correctly identified the original price and the discount amount.
Advanced Percentage Calculations
Beyond the basic percentage formula, there are more complex calculations involving percentages that are useful in various contexts.
1. Percentage Increase and Decrease
To calculate the percentage increase or decrease between two values, use the following formulas:
- Percentage Increase: $\text{Percentage Increase} = \left( \frac{\text{New Value} - \text{Old Value}}{\text{Old Value}} \right) \times 100$
- Percentage Decrease: $\text{Percentage Decrease} = \left( \frac{\text{Old Value} - \text{New Value}}{\text{Old Value}} \right) \times 100$
2. Calculating Percentage of a Percentage
Sometimes, you need to find the percentage of a percentage. To do this, convert both percentages to decimals and multiply them.
- Example: What is 20% of 50%?
- Convert 20% to 0.20 and 50% to 0.50.
- Multiply: $0.20 \times 0.50 = 0.10$
- Convert back to percentage: $0.10 \times 100 = 10%$
- So, 20% of 50% is 10%.
3. Reverse Percentage Calculations
In some cases, you might need to find the original value given a percentage and a resulting value. For example:
- "15% of what number is 30?"
- Let the number be x.
- Set up the equation: $0.15 \times x = 30$
- Solve for x: $x = \frac{30}{0.15} = 200$
- So, 15% of 200 is 30.
Tools and Resources for Percentage Calculations
Several tools and resources can help you with percentage calculations:
1. Online Percentage Calculators
Numerous websites offer free percentage calculators. These tools can quickly solve various percentage problems, including finding percentages, percentage increase/decrease, and more.
2. Spreadsheet Software
Software like Microsoft Excel or Google Sheets can be used to perform percentage calculations. You can enter the values in cells and use formulas to calculate percentages automatically.
- Example: If A1 contains the part and B1 contains the whole, the formula
=A1/B1*100in cell C1 will calculate the percentage.
3. Mobile Apps
Many mobile apps are available for calculating percentages. These apps are convenient for quick calculations on the go.
4. Educational Websites
Websites like Khan Academy and Mathway provide lessons and practice problems on percentages. These resources can help you improve your understanding and skills.
Conclusion
The question "30 of 200 is what percent?" is a basic yet essential percentage problem. By understanding the formula and applying it correctly, we can easily determine that 30 is 15% of 200. Percentages are a fundamental part of mathematics and are crucial for financial literacy, academic performance, data interpretation, health and nutrition, and everyday decision-making. Avoiding common mistakes and using the right tools can further enhance your ability to work with percentages effectively. Whether you're calculating discounts, understanding statistics, or managing your finances, a solid grasp of percentages is invaluable.
Latest Posts
Latest Posts
-
How Many Ounces Are In 250 Ml
Dec 06, 2025
-
How Many Cups Is 28 Oz
Dec 06, 2025
-
How Many Ounces Is 20 Ml
Dec 06, 2025
-
30 Of 200 Is What Percent
Dec 06, 2025
-
6 Hours Ago What Time Was It
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about 30 Of 200 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.