17 Out Of 20 As A Percentage
bemquerermulher
Dec 04, 2025 · 8 min read
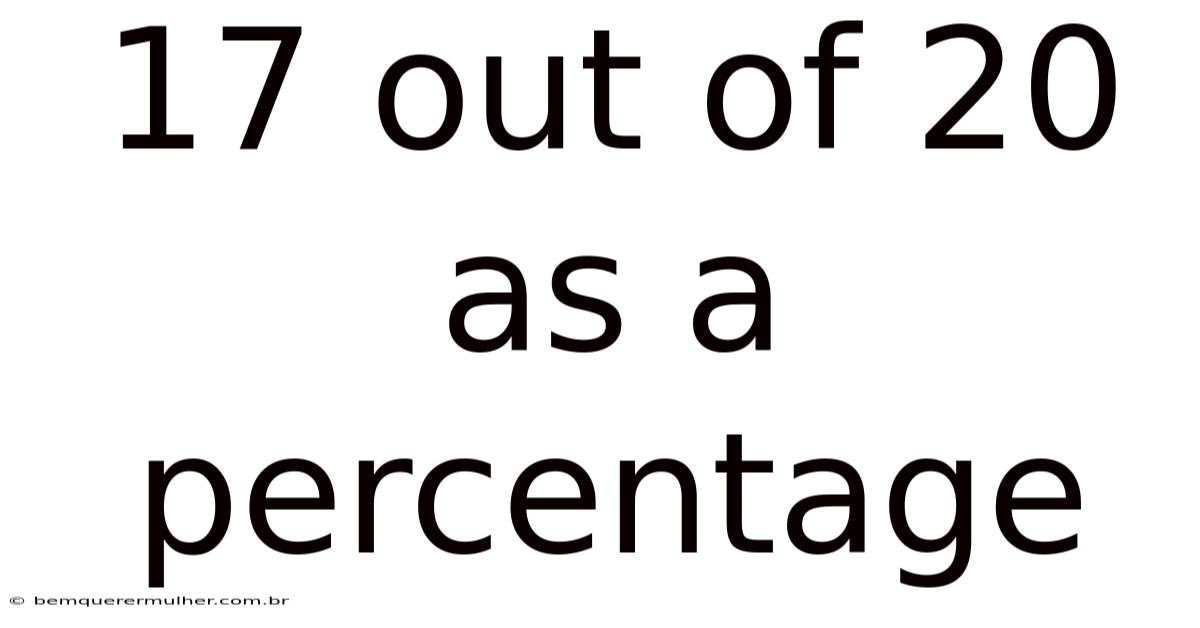
Table of Contents
Here's an in-depth guide on how to calculate 17 out of 20 as a percentage, designed to help anyone easily understand the process and its applications. Whether you're a student, a teacher, or just someone looking to brush up on your math skills, this article will provide you with clear explanations and practical examples.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. In simpler terms, it tells us how many parts out of 100 we have. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Percentages are used everywhere, from calculating discounts at stores to understanding statistics in reports. Knowing how to work with percentages is a fundamental skill in everyday life.
The Basic Formula: Converting a Fraction to a Percentage
To convert any fraction to a percentage, you follow a simple formula:
Percentage = (Fraction) × 100
In this case, our fraction is 17/20. So, to find what percentage 17 out of 20 is, we will multiply this fraction by 100. This formula works because a percentage is essentially the numerator of a fraction whose denominator is 100. By multiplying by 100, we are scaling the fraction to fit this format.
Step-by-Step Calculation: 17 out of 20 as a Percentage
Let's break down the calculation step by step:
Step 1: Write Down the Fraction
First, identify the fraction you want to convert into a percentage. In our scenario, that's 17/20. This fraction represents 17 parts out of a total of 20 parts.
Step 2: Multiply the Fraction by 100
Next, multiply the fraction by 100. This step is crucial as it scales the fraction to represent a value out of 100, which is what a percentage is.
(17/20) × 100
Step 3: Simplify the Expression
To simplify the expression, you can perform the multiplication. You can either multiply 17 by 100 first and then divide by 20, or you can simplify the fraction by dividing 20 into 100. Let’s simplify by dividing 20 into 100:
100 ÷ 20 = 5
Now, multiply 17 by 5:
17 × 5 = 85
Step 4: Add the Percentage Sign
The result of the calculation is 85. To indicate that this number represents a percentage, add the percentage sign (%) to the end.
So, 17 out of 20 as a percentage is 85%.
Alternative Method: Converting the Fraction to a Decimal First
Another way to calculate the percentage is to first convert the fraction to a decimal and then multiply by 100. This method can be particularly useful when dealing with fractions that don't easily simplify.
Step 1: Convert the Fraction to a Decimal
To convert 17/20 to a decimal, divide 17 by 20:
17 ÷ 20 = 0.85
Step 2: Multiply the Decimal by 100
Now, multiply the decimal by 100:
- 85 × 100 = 85
Step 3: Add the Percentage Sign
Add the percentage sign to the result:
85%
As you can see, both methods yield the same result: 17 out of 20 is equal to 85%.
Real-World Applications
Understanding how to calculate percentages is extremely useful in various real-world scenarios. Here are a few examples:
Calculating Grades
In education, percentages are often used to calculate grades. For instance, if a student scores 17 out of 20 on a quiz, their score would be 85%. This allows students and teachers to quickly understand performance relative to the total possible score.
Retail Discounts
When shopping, you often encounter discounts expressed as percentages. For example, a store might offer a 20% discount on an item. Knowing how to calculate percentages helps you determine the actual price you will pay after the discount. If an item costs $20 and there's a 20% discount, you can calculate the discount amount as follows:
Discount Amount = 20% of $20 = (20/100) × $20 = $4 Final Price = $20 - $4 = $16
Financial Calculations
Percentages are fundamental in finance for calculating interest rates, investment returns, and loan amounts. For instance, if you invest $100 and earn a 5% return, you would calculate your earnings as:
Earnings = 5% of $100 = (5/100) × $100 = $5
Statistics and Data Analysis
Percentages are widely used in statistics to represent data in a more understandable format. For example, if a survey shows that 85 out of 100 people prefer a certain product, it can be stated that 85% of the people prefer that product.
Cooking and Baking
In cooking and baking, percentages can help adjust recipes. If a recipe calls for a certain amount of an ingredient and you want to increase or decrease the batch size, you can use percentages to calculate the adjusted amounts.
Common Mistakes to Avoid
When calculating percentages, it's easy to make mistakes. Here are some common pitfalls to avoid:
Misinterpreting the Base
Ensure you understand what the total or base amount is. For example, when calculating a percentage increase, make sure you are using the original amount as the base.
Incorrectly Converting Fractions
When converting fractions to percentages, make sure you perform the division correctly. A small error in division can lead to a significant difference in the final percentage.
Forgetting to Multiply by 100
The most common mistake is forgetting to multiply the fraction or decimal by 100. Without this step, you are not expressing the value as a percentage.
Rounding Errors
When dealing with decimals, rounding errors can occur. Try to maintain as many decimal places as possible until the final step to minimize these errors.
Practice Problems
To solidify your understanding, here are some practice problems:
Problem 1
What percentage is 15 out of 25?
Solution: (15/25) × 100 = 60%
Problem 2
What percentage is 8 out of 10?
Solution: (8/10) × 100 = 80%
Problem 3
What percentage is 3 out of 4?
Solution: (3/4) × 100 = 75%
Problem 4
What percentage is 21 out of 30?
Solution: (21/30) × 100 = 70%
Problem 5
What percentage is 45 out of 50?
Solution: (45/50) × 100 = 90%
Advanced Tips and Tricks
For more advanced calculations and a deeper understanding of percentages, consider the following tips:
Using Percentages to Find Amounts
Sometimes, you need to find an amount when given a percentage. For example, if you know that 30% of a number is 60, you can find the original number as follows:
30% of x = 60 (30/100) × x = 60 x = 60 ÷ (30/100) x = 60 × (100/30) x = 200
Calculating Percentage Increase and Decrease
Percentage increase and decrease are used to show the relative change in a value over time. The formulas are:
Percentage Increase = [(New Value - Original Value) / Original Value] × 100 Percentage Decrease = [(Original Value - New Value) / Original Value] × 100
For example, if a price increases from $20 to $25, the percentage increase is:
Percentage Increase = [($25 - $20) / $20] × 100 = (5/20) × 100 = 25%
Working with Multiple Percentages
When dealing with multiple percentages, be careful to apply them correctly. For example, if an item is discounted by 20% and then an additional 10%, the total discount is not simply 30%. You need to calculate each discount sequentially.
First Discount: 20% off $100 = $20 Price after first discount = $100 - $20 = $80 Second Discount: 10% off $80 = $8 Final Price = $80 - $8 = $72 Total Discount = $100 - $72 = $28 Total Percentage Discount = (28/100) × 100 = 28%
Percentage in Statistics
In statistics, percentages are often used to describe proportions and distributions. Understanding percentages helps in interpreting data and making informed decisions. Here are some key statistical concepts involving percentages:
Descriptive Statistics
Percentages are used in descriptive statistics to summarize data. For example, you might see statements like "60% of respondents agreed with the statement" or "45% of students are female." These percentages provide a clear snapshot of the data.
Inferential Statistics
In inferential statistics, percentages are used to make inferences about a population based on a sample. Confidence intervals, for example, are often expressed as percentages and provide a range within which the true population parameter is likely to fall.
Hypothesis Testing
Percentages are also used in hypothesis testing to compare proportions between different groups. For example, you might test whether the percentage of people who prefer a certain product is significantly different between two demographic groups.
The Importance of Accuracy
Accuracy is crucial when working with percentages. Even small errors can lead to significant misinterpretations or incorrect decisions. Always double-check your calculations and ensure you are using the correct formulas and base values.
In financial contexts, errors in percentage calculations can have significant monetary consequences. In scientific research, inaccurate percentages can lead to flawed conclusions and incorrect interpretations of data.
Conclusion
Calculating 17 out of 20 as a percentage is a straightforward process that involves multiplying the fraction (17/20) by 100. This calculation results in 85%, meaning that 17 out of 20 is equivalent to 85%. Understanding how to calculate percentages is a fundamental skill with wide-ranging applications in everyday life, from calculating grades and discounts to understanding financial data and statistical reports. By following the steps outlined in this guide and practicing with real-world examples, you can master this essential mathematical skill and apply it confidently in various contexts. Whether you are a student, a professional, or simply someone looking to improve your math skills, a solid understanding of percentages will undoubtedly be valuable in numerous aspects of your life.
Latest Posts
Latest Posts
-
How Many Ounces Is 3 Litres
Dec 04, 2025
-
How Many Minutes In 3 Hours
Dec 04, 2025
-
Cells Will Swell When Placed In A Solution That Is
Dec 04, 2025
-
17 Out Of 20 As A Percentage
Dec 04, 2025
-
How Many Seconds Are In 5 Minutes
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about 17 Out Of 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.