15 Of 100 Is What Percent
bemquerermulher
Dec 04, 2025 · 9 min read
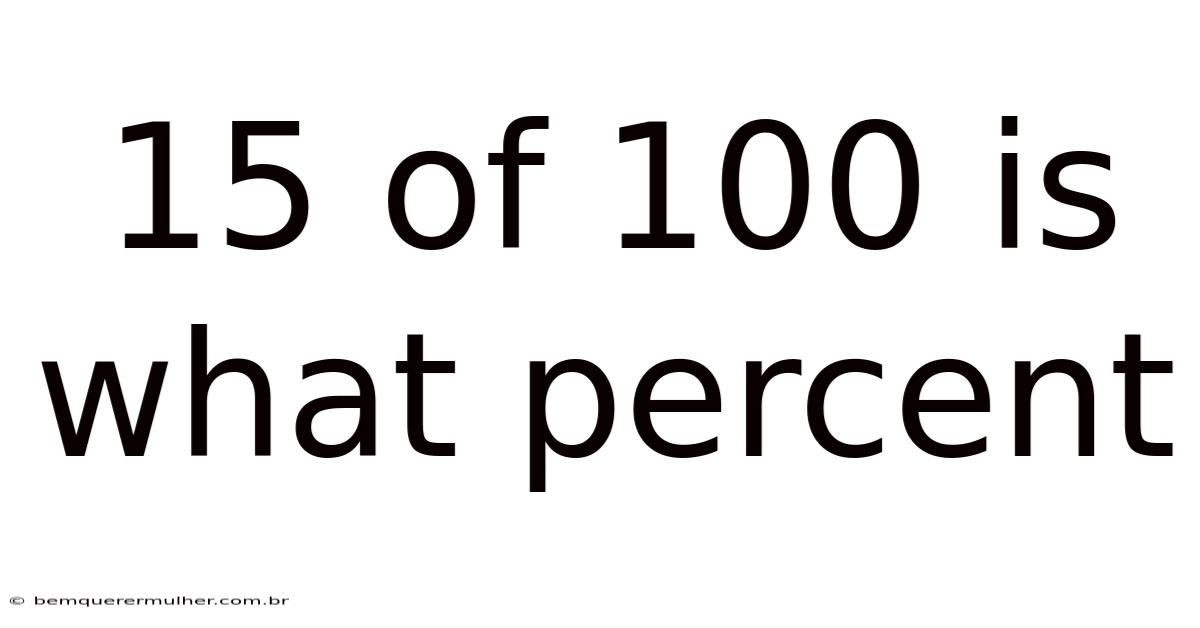
Table of Contents
Fifteen out of one hundred, expressed as "15 of 100," is a fundamental concept in understanding percentages. In essence, it's a way to represent a part of a whole where the whole is standardized to 100. This article will delve into the concept of expressing "15 of 100" as a percentage, explaining the underlying mathematical principles, providing examples, and illustrating its applications in everyday scenarios. Understanding this basic concept is crucial for grasping more complex percentage-related calculations and their significance in various fields.
Introduction
Percentages are a ubiquitous part of modern life. They are used in numerous contexts, from calculating discounts while shopping to understanding statistics in scientific research. At its core, a percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, when we say "15 of 100," we are already very close to expressing it as a percentage. This article will explore how to convert this simple ratio into a percentage and why this conversion is so useful.
Understanding the Basics: What is a Percentage?
A percentage is a dimensionless number, meaning it doesn't have any units. It is a way to express a ratio or fraction with a denominator of 100. The symbol "%" is used to denote percentage. For example, if we say 50%, we mean 50 out of every 100, or 50/100.
Percentages are useful because they provide a standardized way to compare different ratios. For instance, it's easier to compare 15% and 20% than to compare the fractions 15/100 and 20/100 directly, although they represent the same values.
Converting "15 of 100" to a Percentage
The phrase "15 of 100" can be directly translated into a fraction, which is 15/100. To convert this fraction to a percentage, you multiply it by 100%. The calculation is straightforward:
(15/100) * 100% = 15%
So, 15 of 100 is equal to 15%. This means that for every 100 units of the whole, we have 15 units. The simplicity of this conversion is why percentages are so convenient for representing proportions.
Step-by-Step Guide to Converting Any Fraction to a Percentage
While "15 of 100" is already in an easily convertible form, it's useful to know how to convert other fractions to percentages. Here's a step-by-step guide:
- Write the fraction: Identify the fraction you want to convert. For example, let's say you want to convert 3/4 to a percentage.
- Divide the numerator by the denominator: Perform the division to get a decimal. In this case, 3 ÷ 4 = 0.75.
- Multiply by 100%: Multiply the decimal by 100% to convert it to a percentage. So, 0.75 * 100% = 75%.
Therefore, 3/4 is equal to 75%. This method works for any fraction, whether it's simple or complex.
Why Percentages are Useful: Practical Applications
Percentages are used in a wide variety of fields and everyday situations. Here are some examples:
- Finance: Interest rates on loans and savings accounts are expressed as percentages. For example, a loan with a 5% annual interest rate means you pay 5% of the loan amount each year as interest.
- Retail: Discounts are often given as percentages. A 20% off sale means that an item's price is reduced by 20% of its original value.
- Statistics: Percentages are used to describe data. For instance, a survey might show that 60% of respondents prefer a certain product.
- Education: Grades are often expressed as percentages. A score of 85% on a test means you answered 85 out of 100 questions correctly.
- Health: Body fat percentage is used as a measure of health. It represents the proportion of your body weight that is fat.
Examples and Practice Problems
To solidify your understanding, let's go through some examples and practice problems:
Example 1: Calculating a Discount
A shirt costs $40, and there is a 25% discount. How much will you save?
- Calculate 25% of $40: (25/100) * $40 = 0.25 * $40 = $10
- You will save $10 on the shirt.
Example 2: Determining a Percentage of a Quantity
If you have 200 apples and 30% of them are green, how many green apples do you have?
- Calculate 30% of 200: (30/100) * 200 = 0.30 * 200 = 60
- You have 60 green apples.
Practice Problem 1
Convert 7/10 to a percentage.
Practice Problem 2
What is 40% of 150?
Solutions
- Practice Problem 1: (7/10) * 100% = 0.7 * 100% = 70%
- Practice Problem 2: (40/100) * 150 = 0.4 * 150 = 60
Common Mistakes to Avoid
When working with percentages, there are some common mistakes to watch out for:
- Forgetting to multiply by 100%: When converting a decimal or fraction to a percentage, always remember to multiply by 100%.
- Misinterpreting the base: Make sure you know what the "whole" or base is when calculating a percentage. For example, if you're calculating a percentage increase, the base is the original value, not the new value.
- Adding or subtracting percentages incorrectly: You can't simply add or subtract percentages unless they are percentages of the same base. For example, a 10% increase followed by a 10% decrease does not result in the original value.
Advanced Concepts: Percentage Change
Percentage change is a way to describe how much a quantity has increased or decreased. It is calculated using the formula:
Percentage Change = [(New Value - Old Value) / Old Value] * 100%
If the result is positive, it's a percentage increase. If it's negative, it's a percentage decrease.
Example: Calculating Percentage Increase
A stock's price increased from $50 to $60. What is the percentage increase?
- Percentage Change = [($60 - $50) / $50] * 100% = ($10 / $50) * 100% = 0.2 * 100% = 20%
- The stock's price increased by 20%.
Example: Calculating Percentage Decrease
A store reduced the price of a TV from $500 to $400. What is the percentage decrease?
- Percentage Change = [($400 - $500) / $500] * 100% = (-$100 / $500) * 100% = -0.2 * 100% = -20%
- The TV's price decreased by 20%.
Real-World Applications in Detail
Percentages play a critical role in various sectors, offering a standardized way to interpret data and make informed decisions. Here's a more detailed look at some real-world applications:
Finance and Investing
In finance, percentages are fundamental. Interest rates, investment returns, and expense ratios are all expressed as percentages. For example, understanding the annual percentage yield (APY) on a savings account helps consumers compare different savings options. Similarly, investors use percentage gains and losses to evaluate the performance of their portfolios. Expense ratios, which represent the percentage of assets paid out for fund operating expenses, are crucial for assessing the cost-effectiveness of mutual funds and ETFs.
Retail and Sales
Retailers heavily rely on percentages for pricing strategies and marketing. Discounts, markups, and profit margins are all calculated using percentages. A "30% off" sale can significantly impact consumer behavior, and retailers carefully analyze these promotions to maximize sales while maintaining profitability. Sales tax is also calculated as a percentage of the purchase price, adding another layer of percentage-based calculations in retail transactions.
Healthcare and Medicine
In healthcare, percentages are used to describe the effectiveness of treatments, prevalence of diseases, and patient outcomes. For example, a clinical trial might report that a new drug is "80% effective" in treating a particular condition. This percentage represents the proportion of patients who experienced a positive outcome from the treatment. Percentages are also used to track vaccination rates, infection rates, and other key health indicators, providing critical information for public health initiatives.
Education and Assessment
Education systems use percentages to assess student performance and track academic progress. Grades are often expressed as percentages, providing a standardized way to evaluate student achievement. Standardized tests, such as the SAT or ACT, use percentile ranks to compare a student's performance to that of other test-takers. These percentile scores indicate the percentage of students who scored below a particular student, offering a clear measure of relative performance.
Environmental Science
Environmental scientists use percentages to monitor pollution levels, track deforestation rates, and assess the impact of climate change. For example, reports might state that "carbon emissions increased by 5% this year," providing a quantitative measure of environmental impact. Percentages are also used to describe the composition of the atmosphere, the proportion of renewable energy sources, and the percentage of land covered by forests.
The Psychology of Percentages
The way percentages are presented can significantly influence people's perceptions and decisions. This is because percentages are often used in framing effects, where the same information is presented in different ways to alter people's judgments. For example, a product described as "90% fat-free" is often perceived more favorably than one described as "contains 10% fat," even though both statements convey the same information.
Understanding this psychological aspect is crucial for both consumers and marketers. Consumers need to be aware of how percentages are used to influence their decisions, and marketers need to use percentages ethically and responsibly.
Tips for Mastering Percentage Calculations
To become proficient in working with percentages, consider the following tips:
- Practice regularly: The more you practice percentage calculations, the more comfortable you will become with them.
- Use real-world examples: Apply percentage calculations to everyday situations, such as calculating discounts or tips.
- Understand the base: Always identify the "whole" or base when calculating a percentage.
- Double-check your work: Make sure your calculations are accurate, especially when dealing with complex problems.
- Use a calculator: Don't hesitate to use a calculator for complex calculations, but make sure you understand the underlying concepts.
The Importance of Understanding Ratios and Proportions
Percentages are closely related to ratios and proportions. A ratio is a comparison of two quantities, while a proportion is an equation stating that two ratios are equal. Understanding these concepts is essential for mastering percentage calculations.
For example, if you know that the ratio of boys to girls in a class is 3:2, you can use this information to calculate the percentage of boys and girls in the class. To do this, you first find the total number of parts in the ratio (3 + 2 = 5). Then, you divide each part by the total to get a fraction (3/5 for boys and 2/5 for girls). Finally, you convert these fractions to percentages (60% boys and 40% girls).
Conclusion
The concept of "15 of 100" being equal to 15% is a foundational element in understanding percentages. This simple conversion is a cornerstone for numerous applications across finance, retail, statistics, and everyday life. By grasping the basic principles, practicing calculations, and avoiding common mistakes, anyone can become proficient in using percentages to interpret data, make informed decisions, and solve real-world problems. Whether you're calculating discounts, analyzing statistics, or tracking personal finances, a solid understanding of percentages is an invaluable skill. Mastering percentages is not just about performing calculations; it's about developing a critical thinking skill that empowers you to navigate the quantitative aspects of the world around you.
Latest Posts
Latest Posts
-
What Is A 40 Out Of 50
Dec 04, 2025
-
Levels Of Organization In An Ecosystem
Dec 04, 2025
-
40 Inch Is How Many Feet
Dec 04, 2025
-
15 Of 100 Is What Percent
Dec 04, 2025
-
How Many Ounces Are In A 1 2 Cup
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 100 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.