12 Out Of 15 As A Percentage
bemquerermulher
Dec 03, 2025 · 10 min read
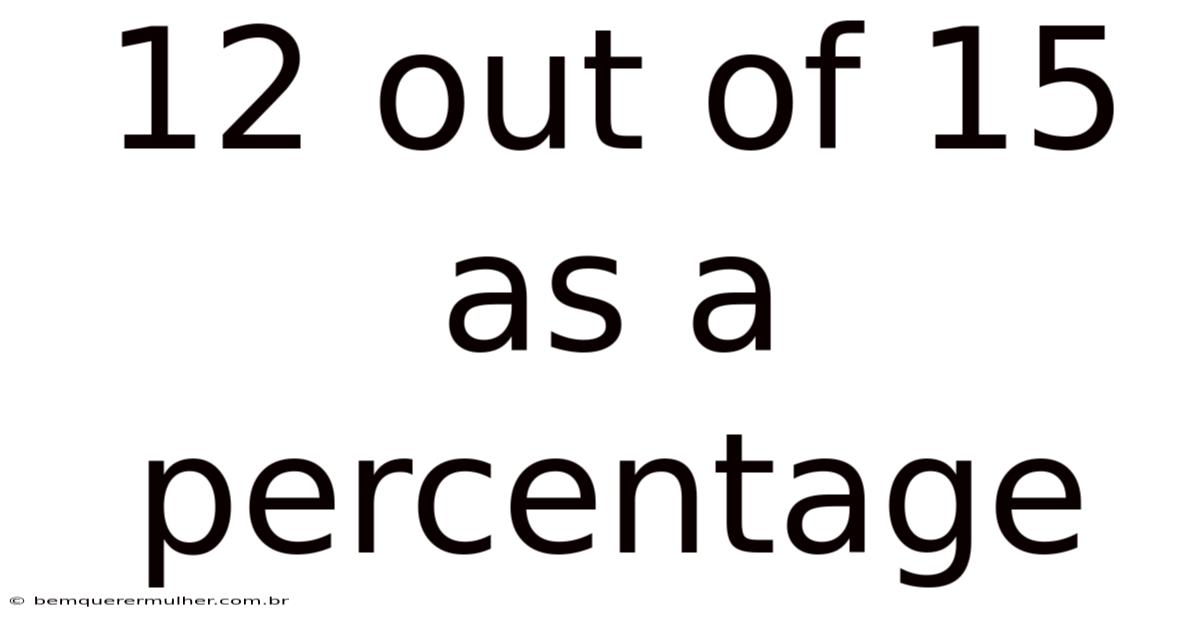
Table of Contents
Here's a comprehensive guide on how to calculate 12 out of 15 as a percentage, making it easy to understand with step-by-step instructions and real-world examples. This article provides a clear explanation suitable for students and anyone needing to improve their percentage calculation skills.
Calculating 12 Out of 15 as a Percentage: A Comprehensive Guide
Percentages are a fundamental concept in mathematics, used extensively in everyday life from calculating discounts while shopping to understanding statistical data. Knowing how to convert a fraction into a percentage is a valuable skill. This article focuses on how to calculate what percentage 12 is of 15, providing a clear, step-by-step explanation along with practical examples to help you grasp the concept thoroughly.
Introduction to Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Percentages are used to express how large one quantity is relative to another quantity. To find a percentage, you typically divide the value you are interested in (in this case, 12) by the total value (in this case, 15), and then multiply the result by 100.
Step-by-Step Calculation
Calculating what percentage 12 is of 15 involves a straightforward process. Here’s a detailed breakdown:
-
Form the Fraction: The first step is to express the given values as a fraction. In this scenario, you want to find what percentage 12 is of 15, so you write it as a fraction:
12 / 15 -
Divide the Numerator by the Denominator: Next, you divide the numerator (the top number) by the denominator (the bottom number). This will give you a decimal:
12 ÷ 15 = 0.8 -
Multiply by 100: To convert the decimal to a percentage, multiply the result by 100:
0.8 × 100 = 80 -
Add the Percentage Symbol: Finally, add the percentage symbol (%) to the result to denote that it is a percentage:
80%
Therefore, 12 out of 15 as a percentage is 80%.
Detailed Explanation of Each Step
To ensure complete understanding, let’s delve deeper into each step of the calculation.
Step 1: Forming the Fraction
The fraction represents the part of the whole that you are interested in. In this case, 12 is the part, and 15 is the whole. Writing it as 12/15 allows you to see the relationship between these two numbers clearly.
Step 2: Dividing the Numerator by the Denominator
Dividing 12 by 15 converts the fraction into a decimal. This decimal represents the proportion of 15 that 12 constitutes. The division is performed as follows:
0.8
15|12.0
12.0
-----
0.0
The result, 0.8, indicates that 12 is 0.8 times 15.
Step 3: Multiplying by 100
Multiplying the decimal by 100 converts it into a percentage. This is because a percentage is defined as a number out of 100. Multiplying by 100 effectively scales the decimal to represent the number out of 100:
0. 8 × 100 = 80
This means that 12 is 80 out of 100, which is the definition of a percentage.
Step 4: Adding the Percentage Symbol
Adding the percentage symbol (%) is crucial because it clarifies that the number is a percentage and not just a regular number. It’s a standard notation that signifies the value is expressed as a part of 100.
Alternative Method: Simplifying the Fraction First
Another approach to calculating the percentage is to simplify the fraction before performing the division. This can make the numbers easier to work with, especially if you don't have a calculator handy.
-
Simplify the Fraction: Look for common factors between the numerator and the denominator. In this case, both 12 and 15 are divisible by 3. Divide both numbers by 3:
12 ÷ 3 = 4 15 ÷ 3 = 5So, the simplified fraction is:
4 / 5 -
Divide the Simplified Numerator by the Denominator: Now, divide the simplified numerator by the simplified denominator:
4 ÷ 5 = 0.8 -
Multiply by 100: Multiply the result by 100 to convert the decimal to a percentage:
0.8 × 100 = 80 -
Add the Percentage Symbol: Add the percentage symbol to the result:
80%
As you can see, simplifying the fraction first yields the same result: 80%.
Real-World Examples
To further illustrate the concept, let’s look at some real-world examples where calculating 12 out of 15 as a percentage might be useful.
-
Test Scores: Imagine you took a quiz with 15 questions, and you answered 12 of them correctly. To find out your score as a percentage:
- You got 12 out of 15 questions right.
- 12/15 = 0.8
- 0.8 * 100 = 80%
- Therefore, you scored 80% on the quiz.
-
Sales Targets: Suppose a salesperson has a target of making 15 sales in a week and they make 12 sales. To calculate the percentage of their target achieved:
- They achieved 12 out of 15 sales.
- 12/15 = 0.8
- 0.8 * 100 = 80%
- Thus, they achieved 80% of their sales target.
-
Resource Allocation: A project manager needs to allocate resources, and out of 15 available resources, 12 are allocated to a specific task. To find the percentage of resources allocated:
- 12 out of 15 resources are allocated.
- 12/15 = 0.8
- 0.8 * 100 = 80%
- So, 80% of the resources are allocated to the task.
-
Inventory: A store has 15 items of a particular product in stock, and 12 of them are sold. To calculate the percentage of the product sold:
- 12 out of 15 items were sold.
- 12/15 = 0.8
- 0.8 * 100 = 80%
- Therefore, 80% of the product was sold.
Common Mistakes to Avoid
When calculating percentages, it’s easy to make mistakes if you’re not careful. Here are some common errors to watch out for:
-
Incorrect Fraction Setup: Ensure that you set up the fraction correctly with the part you’re interested in as the numerator and the total as the denominator. Reversing these can lead to an incorrect percentage.
-
Miscalculation During Division: Double-check your division to avoid errors. A small mistake in division can significantly affect the final percentage.
-
Forgetting to Multiply by 100: One of the most common mistakes is forgetting to multiply the decimal by 100. This step is essential for converting the decimal to a percentage.
-
Omitting the Percentage Symbol: Always include the percentage symbol (%) to clearly indicate that the number is a percentage and not a regular value.
-
Rounding Errors: If the decimal result is long, be mindful of how you round the numbers. Incorrect rounding can lead to inaccuracies in the final percentage.
The Importance of Understanding Percentages
Understanding percentages is crucial for several reasons:
-
Financial Literacy: Percentages are used extensively in finance, from calculating interest rates on loans to understanding investment returns.
-
Data Analysis: In various fields, including science, business, and social sciences, percentages are used to analyze data and draw meaningful conclusions.
-
Everyday Decision Making: From shopping discounts to understanding statistics in the news, percentages help you make informed decisions every day.
-
Academic Success: Percentages are a core concept in mathematics and are essential for success in various academic subjects.
Advanced Tips and Tricks
Here are some advanced tips and tricks to help you work with percentages more efficiently:
-
Using Benchmarks: Familiarize yourself with common percentage benchmarks such as 25%, 50%, and 75%. These can help you quickly estimate percentages without doing detailed calculations.
-
Converting Percentages to Fractions: Knowing how to convert percentages back to fractions can be useful in certain situations. For example, 80% can be written as 80/100, which simplifies to 4/5.
-
Using Percentages in Ratios: Percentages can be used to express ratios. For instance, if 12 out of 15 students passed an exam, you can say that the ratio of students who passed to the total number of students is 80%.
Practical Exercises
To reinforce your understanding, here are some practical exercises:
- Exercise 1: What percentage is 24 out of 30?
- Exercise 2: What percentage is 9 out of 12?
- Exercise 3: What percentage is 15 out of 20?
- Exercise 4: What percentage is 6 out of 8?
- Exercise 5: What percentage is 18 out of 25?
Answers:
- 80%
- 75%
- 75%
- 75%
- 72%
Understanding Percentage Increase and Decrease
While this article focuses on calculating a basic percentage, it's also important to understand percentage increase and decrease. These concepts are used to describe how much a quantity has changed relative to its initial value.
Percentage Increase
Percentage increase is used when a quantity increases from an initial value to a final value. The formula to calculate percentage increase is:
Percentage Increase = [(Final Value - Initial Value) / Initial Value] * 100
Example: If a price increases from $15 to $18, the percentage increase is:
[(18 - 15) / 15] * 100 = (3 / 15) * 100 = 0.2 * 100 = 20%
So, the price increased by 20%.
Percentage Decrease
Percentage decrease is used when a quantity decreases from an initial value to a final value. The formula to calculate percentage decrease is:
Percentage Decrease = [(Initial Value - Final Value) / Initial Value] * 100
Example: If a price decreases from $15 to $12, the percentage decrease is:
[(15 - 12) / 15] * 100 = (3 / 15) * 100 = 0.2 * 100 = 20%
Thus, the price decreased by 20%.
The Use of Online Calculators
While understanding the manual calculation of percentages is essential, online percentage calculators can be useful tools for quick and accurate results. These calculators can handle complex calculations and are readily available on the internet. However, it's important to verify the results and understand the underlying principles to ensure accuracy.
FAQ Section
Q: Why are percentages important? A: Percentages are important because they provide a standardized way to compare different quantities and understand proportions. They are used in various fields, including finance, statistics, and everyday decision-making.
Q: Can a percentage be greater than 100%? A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a final value to an initial value where the final value is more than double the initial value. For example, if a company's revenue doubles, it has increased by 100%. If it more than doubles, the increase is over 100%.
Q: How do I convert a percentage to a decimal? A: To convert a percentage to a decimal, divide the percentage by 100. For example, 80% becomes 0.8 when divided by 100.
Q: What is the difference between percentage and percentile? A: A percentage is a ratio that represents a part of 100, while a percentile is a measure used in statistics indicating the value below which a given percentage of observations in a group of observations falls.
Q: How can I improve my percentage calculation skills? A: Practice regularly with different examples and real-world scenarios. Use online resources and tools to check your answers and reinforce your understanding.
Conclusion
Calculating what percentage 12 is of 15 is a fundamental mathematical skill with numerous practical applications. By following the step-by-step instructions outlined in this article—forming the fraction, dividing, multiplying by 100, and adding the percentage symbol—anyone can master this calculation. Remember to avoid common mistakes and practice regularly to improve your skills. Understanding percentages is not just an academic exercise; it’s a valuable tool that enhances your ability to make informed decisions in various aspects of life.
Latest Posts
Latest Posts
-
How Many Oz In 500 Ml
Dec 03, 2025
-
How Many Seconds In 2 Hours
Dec 03, 2025
-
12 Out Of 15 As A Percentage
Dec 03, 2025
-
How Many Hours Is 150 Minutes
Dec 03, 2025
-
How Many Minutes Are In 4 Hours
Dec 03, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 15 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.