What Percent Of 16 Is 20
bemquerermulher
Dec 04, 2025 · 7 min read
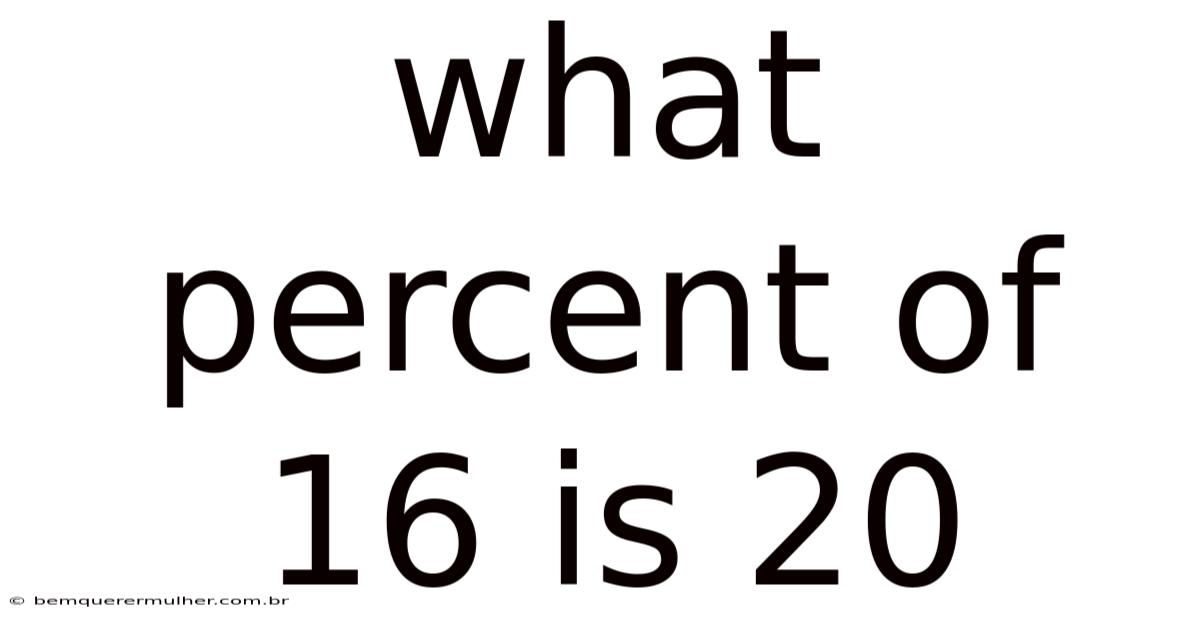
Table of Contents
The question "What percent of 16 is 20?" is a common type of percentage problem encountered in mathematics. To solve it, we need to determine what percentage 16 represents when compared to 20. This involves setting up a proportion and solving for the unknown percentage. Understanding how to solve these types of problems is useful not only in academic settings but also in everyday situations like calculating discounts, comparing prices, or understanding financial data. In this article, we will explore different methods to solve this problem, provide clear, step-by-step instructions, and delve into the mathematical principles underlying the calculation.
Understanding Percentages
Before diving into the solution, it's important to understand what a percentage represents. A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "per hundred." Therefore, when we say "x percent," we mean x/100. Percentages are used to express relative changes, compare quantities, and understand proportions in a standardized way.
Method 1: Direct Calculation
One of the most straightforward methods to find what percent of 16 is 20 involves setting up a simple algebraic equation. The problem can be phrased as:
"x% of 16 is 20."
In mathematical terms, this translates to:
(x/100) * 16 = 20
To solve for x, we can follow these steps:
-
Write the Equation: Start by writing the equation that represents the problem:
(x/100) * 16 = 20
-
Isolate x: To isolate x, we need to undo the operations that are being performed on it. First, we can multiply both sides of the equation by 100 to get rid of the fraction:
x * 16 = 20 * 100
x * 16 = 2000
-
Solve for x: Next, divide both sides by 16 to solve for x:
x = 2000 / 16
x = 125
So, 20 is 125% of 16.
Method 2: Using Proportions
Another method to solve this problem involves setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the proportion as follows:
16 / 100 = 20 / x
Here, we are comparing 16 to 100% and setting it equal to the ratio of 20 to the unknown percentage x.
To solve for x, we can use cross-multiplication:
-
Set up the Proportion: Write the proportion equation:
16 / 100 = 20 / x
-
Cross-Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa:
16 * x = 20 * 100
16x = 2000
-
Solve for x: Divide both sides by 16 to isolate x:
x = 2000 / 16
x = 125
Again, we find that 20 is 125% of 16.
Method 3: Direct Division and Multiplication
A third method is to divide 20 by 16 and then multiply the result by 100 to get the percentage directly. This method is based on the idea that the percentage is the ratio of the two numbers expressed as a percentage:
-
Divide: Divide 20 by 16:
20 / 16 = 1.25
-
Multiply by 100: Multiply the result by 100 to convert it to a percentage:
- 25 * 100 = 125%
This method confirms that 20 is 125% of 16.
Real-World Applications
Understanding how to calculate percentages is extremely useful in various real-world scenarios:
- Finance: When dealing with investments, returns, or interest rates, percentages help in understanding the growth or decline of investments.
- Retail: Discounts and sales are often expressed as percentages. Knowing how to calculate these can help you determine the actual savings.
- Statistics: Percentages are used to present data in a clear and understandable manner, such as in survey results or demographic information.
- Cooking: Recipes often require adjusting ingredient quantities, and understanding percentages can help scale recipes accurately.
Common Mistakes to Avoid
When working with percentages, it's important to avoid common mistakes that can lead to incorrect answers:
- Misunderstanding the Base: Always be clear about what number you are taking the percentage of. In the problem "What percent of 16 is 20?", 16 is the base.
- Incorrect Setup: Setting up the equation or proportion incorrectly can lead to wrong answers. Double-check your setup to ensure it accurately represents the problem.
- Calculation Errors: Simple arithmetic errors can throw off your final answer. Use a calculator or double-check your calculations to avoid mistakes.
- Forgetting to Multiply by 100: When finding a percentage, remember to multiply the decimal result by 100 to express it as a percentage.
Practice Problems
To reinforce your understanding, here are a few practice problems:
- What percent of 25 is 30?
- What percent of 50 is 60?
- What percent of 80 is 100?
Solutions to Practice Problems
-
What percent of 25 is 30?
- Using the equation method: (x/100) * 25 = 30
- Solving for x: x = (30 * 100) / 25
- x = 3000 / 25
- x = 120%
So, 30 is 120% of 25.
-
What percent of 50 is 60?
- Using the equation method: (x/100) * 50 = 60
- Solving for x: x = (60 * 100) / 50
- x = 6000 / 50
- x = 120%
So, 60 is 120% of 50.
-
What percent of 80 is 100?
- Using the equation method: (x/100) * 80 = 100
- Solving for x: x = (100 * 100) / 80
- x = 10000 / 80
- x = 125%
So, 100 is 125% of 80.
Advanced Concepts: Percentage Increase and Decrease
Understanding percentage increase and decrease is also essential when dealing with percentages.
-
Percentage Increase: The percentage increase is the extent to which a quantity increases. It is calculated by:
Percentage Increase = [(New Value - Original Value) / Original Value] * 100
-
Percentage Decrease: The percentage decrease is the extent to which a quantity decreases. It is calculated by:
Percentage Decrease = [(Original Value - New Value) / Original Value] * 100
For example, if a price increases from $16 to $20, the percentage increase is:
Percentage Increase = [(20 - 16) / 16] * 100 = (4 / 16) * 100 = 25%
Using Calculators and Tools
In many cases, you can use calculators or online tools to quickly find the percentage. Most calculators have a percentage function that simplifies the process. Online percentage calculators can be found with a quick search and can be useful for double-checking your work or solving complex problems.
The Importance of Precision
When working with percentages, precision is crucial, especially in fields like finance and science. Even small rounding errors can lead to significant discrepancies in the final results. Therefore, it's important to use as many decimal places as possible during calculations and only round the final answer if necessary.
Understanding the Concept of Base
The concept of the base is fundamental in percentage problems. The base is the reference value to which the percentage is applied. In the question "What percent of 16 is 20?", 16 is the base. Identifying the base correctly is crucial for setting up the problem and solving it accurately.
Expanding on Different Types of Percentage Problems
There are several types of percentage problems, and understanding each type can help you solve a wide range of real-world scenarios:
- Finding a Percentage of a Number: This involves finding what a specific percentage of a number is. For example, what is 20% of 50?
- Finding What Percentage One Number Is of Another: This involves finding what percentage one number represents of another, as in our original problem.
- Finding the Whole When Given a Percentage: This involves finding the whole amount when you know a percentage of it. For example, if 30% of a number is 60, what is the number?
Tips for Mastering Percentage Problems
- Practice Regularly: The more you practice, the more comfortable you will become with percentage problems.
- Understand the Concepts: Make sure you have a solid understanding of what percentages represent and how they are calculated.
- Break Down the Problem: Break complex problems into smaller, more manageable steps.
- Check Your Work: Always double-check your calculations to avoid errors.
- Use Real-World Examples: Relate percentage problems to real-world scenarios to better understand their practical applications.
Conclusion
In summary, determining what percent of 16 is 20 involves understanding the basic principles of percentages and applying algebraic or proportional methods to solve for the unknown percentage. By setting up the problem correctly, performing accurate calculations, and avoiding common mistakes, we can confidently conclude that 20 is 125% of 16. This knowledge is not only valuable in academic settings but also in everyday life, where understanding percentages is essential for making informed decisions in various contexts, from finance to retail. Mastering these calculations enhances our ability to analyze and interpret quantitative data, making us more informed and effective individuals.
Latest Posts
Latest Posts
-
How Many Oz Are In A Liter
Dec 04, 2025
-
200 Degrees C Is What In Fahrenheit
Dec 04, 2025
-
How Much Is 6 Oz In Cups
Dec 04, 2025
-
How To Change A Decimal To A Fraction
Dec 04, 2025
-
What Time Will It Be In 16 Hours
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 16 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.