What Is The Percentage Of 1/8
bemquerermulher
Dec 03, 2025 · 9 min read
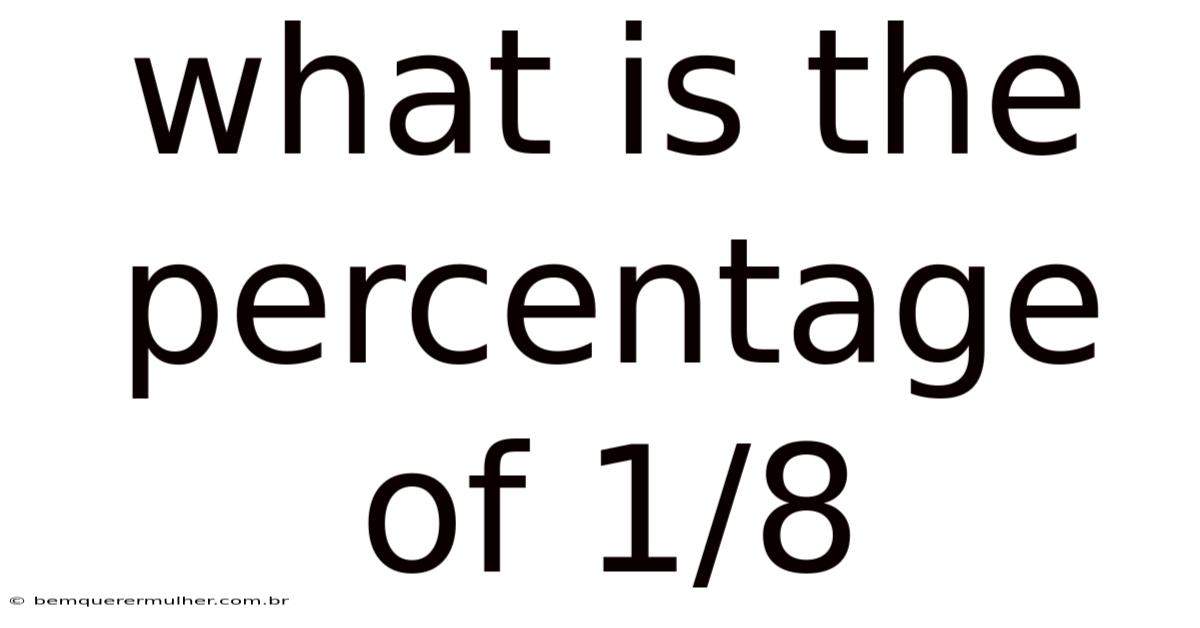
Table of Contents
The percentage of 1/8 is a simple yet fundamental concept in mathematics, bridging the gap between fractions and percentages. Understanding how to convert fractions to percentages is crucial in everyday life, from calculating discounts while shopping to interpreting statistical data. In this article, we will thoroughly explore how to determine what percentage 1/8 represents, provide a step-by-step guide, offer practical examples, and discuss the broader applications of this mathematical conversion.
Introduction
Converting fractions to percentages is a common task in various fields, including finance, statistics, and everyday problem-solving. A percentage is essentially a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." Therefore, when we ask, "What is the percentage of 1/8?", we are essentially asking, "How much is 1/8 out of 100?"
Understanding this conversion helps in interpreting data more intuitively. For example, if a study reports that 1/8 of participants experienced a certain effect, knowing that this is equivalent to 12.5% makes the information more relatable and easier to grasp. This article will guide you through the process of converting 1/8 to a percentage, explain the underlying mathematical principles, and illustrate why this skill is valuable.
Step-by-Step Guide to Converting 1/8 to a Percentage
Converting the fraction 1/8 to a percentage involves a straightforward process. Here’s a detailed, step-by-step guide to help you understand and perform this conversion:
-
Understand the Basics:
- A percentage is a way of expressing a number as a fraction of 100.
- To convert a fraction to a percentage, you need to express the fraction as an equivalent fraction with a denominator of 100 or multiply the fraction by 100%.
-
Set Up the Conversion:
- You start with the fraction 1/8.
- To convert this to a percentage, you will multiply it by 100%.
-
Perform the Calculation:
- Multiply the fraction by 100%:
- (1/8) * 100%
- Multiply the fraction by 100%:
-
Simplify the Expression:
- To simplify, you can divide 100 by 8:
- 100 ÷ 8 = 12.5
- To simplify, you can divide 100 by 8:
-
State the Result:
- Therefore, 1/8 is equal to 12.5%.
Example Calculation
To illustrate, let's go through the calculation again:
- Start with the fraction: 1/8
- Multiply by 100%: (1/8) * 100%
- Divide 100 by 8: 100 ÷ 8 = 12.5
- Result: 1/8 = 12.5%
By following these steps, you can confidently convert the fraction 1/8 to its percentage equivalent, which is 12.5%.
The Mathematical Explanation Behind the Conversion
The process of converting a fraction to a percentage relies on the fundamental principles of mathematics. Here’s a more detailed explanation of the underlying math:
-
Understanding Fractions:
- A fraction represents a part of a whole. In the fraction 1/8, the numerator (1) represents the part, and the denominator (8) represents the whole.
-
Percentages as Fractions:
- A percentage is a ratio that represents a fraction out of 100. For example, 50% means 50 out of 100, or 50/100.
-
Conversion Process:
- To convert a fraction to a percentage, you multiply the fraction by 100%. This is because you want to find out how many parts out of 100 the fraction represents.
-
Mathematical Justification:
- When you multiply 1/8 by 100%, you are essentially finding an equivalent fraction with a denominator of 100.
- The equation is:
- (1/8) * 100% = (1 * 100) / 8 % = 100/8 %
- Dividing 100 by 8 gives you 12.5, so the equivalent percentage is 12.5%.
-
Alternative Method:
- Another way to understand this is by converting the fraction 1/8 to a decimal first and then to a percentage.
- To convert 1/8 to a decimal, divide 1 by 8:
- 1 ÷ 8 = 0.125
- To convert the decimal to a percentage, multiply by 100:
-
- 125 * 100% = 12.5%
-
Both methods yield the same result, demonstrating the consistency of mathematical principles in converting fractions to percentages.
Practical Examples and Applications
Understanding that 1/8 is equal to 12.5% has numerous practical applications in everyday life and various professional fields. Here are some examples:
-
Discounts and Sales:
- Imagine a store is offering a discount of 1/8 off the original price of an item. If the original price is $80, you can quickly calculate the discount amount by knowing that 1/8 is 12.5%.
- Discount amount = 12.5% of $80 = 0.125 * $80 = $10
- So, the item is $10 off, making the new price $70.
-
Cooking and Baking:
- Recipes often use fractions to indicate ingredient quantities. If a recipe calls for 1/8 of a cup of an ingredient, knowing that this is 12.5% of a cup can help you measure accurately.
- For example, if a cup is 240 ml, then 1/8 of a cup is 12.5% of 240 ml = 0.125 * 240 ml = 30 ml.
-
Financial Investments:
- In finance, understanding fractions and percentages is crucial for calculating returns on investments.
- If an investment increases by 1/8 of its original value, it means it has increased by 12.5%. If the initial investment was $1000, the increase is 12.5% of $1000 = 0.125 * $1000 = $125.
-
Statistical Analysis:
- In statistical analysis, fractions and percentages are used to represent proportions of data. If a survey finds that 1/8 of respondents prefer a certain product, knowing that this is 12.5% helps in interpreting the data.
-
Real Estate:
- When calculating property taxes or commissions, fractions and percentages are frequently used. If a real estate agent earns a commission of 1/8 of the sale price, knowing this is 12.5% helps in determining the commission amount.
-
Academic Studies:
- Students often encounter fractions and percentages in various subjects, including mathematics, science, and economics. Converting fractions to percentages is essential for solving problems and understanding concepts.
These examples illustrate the practical relevance of understanding how to convert fractions to percentages, especially the fraction 1/8.
Common Mistakes to Avoid
When converting fractions to percentages, several common mistakes can occur. Being aware of these mistakes can help you avoid errors and ensure accurate conversions.
-
Forgetting to Multiply by 100%:
- The most common mistake is forgetting to multiply the fraction by 100%. To convert a fraction to a percentage, you must multiply it by 100%. For example, simply stating that 1/8 is 0.125 without converting it to 12.5% is incorrect.
-
Incorrectly Dividing:
- When dividing to convert a fraction to a decimal, ensure that you divide the numerator by the denominator correctly. For 1/8, dividing 1 by 8 should yield 0.125. An incorrect division will lead to an incorrect percentage.
-
Misunderstanding the Concept of Percentage:
- Some people may not fully understand that a percentage represents a part out of 100. This misunderstanding can lead to errors in converting fractions to percentages. Remember that "percent" means "per hundred," so you are finding how many parts out of 100 the fraction represents.
-
Rounding Errors:
- When dealing with fractions that result in repeating decimals, rounding errors can occur. While rounding may be necessary, it's important to round to an appropriate number of decimal places to maintain accuracy. For example, if a fraction converts to 0.3333..., rounding to 33% might be acceptable for quick estimations, but for precise calculations, using more decimal places (e.g., 33.33%) is better.
-
Confusing Fractions and Percentages:
- Sometimes, people confuse fractions with percentages and may not recognize when a conversion is needed. Always remember that a fraction represents a part of a whole, while a percentage represents a part out of 100.
-
Not Simplifying Fractions First:
- Although not always necessary, simplifying a fraction before converting it to a percentage can sometimes make the calculation easier. For example, if you have the fraction 2/16, simplifying it to 1/8 before converting can reduce the complexity of the division.
By being mindful of these common mistakes, you can improve your accuracy and confidence in converting fractions to percentages.
Advanced Tips for Percentage Conversions
While the basic method for converting fractions to percentages is straightforward, there are advanced tips and techniques that can help you perform these conversions more efficiently and accurately.
-
Using Benchmarks:
- Memorizing common fraction-to-percentage conversions can serve as benchmarks for estimating other conversions. For example, knowing that:
- 1/2 = 50%
- 1/4 = 25%
- 1/8 = 12.5%
- 1/10 = 10%
- These benchmarks can help you quickly estimate the percentages of related fractions.
- Memorizing common fraction-to-percentage conversions can serve as benchmarks for estimating other conversions. For example, knowing that:
-
Converting to Decimals First:
- As mentioned earlier, converting a fraction to a decimal before converting it to a percentage can sometimes be easier. Divide the numerator by the denominator to get the decimal, then multiply by 100 to get the percentage.
- Example: Convert 3/8 to a percentage.
- 3 ÷ 8 = 0.375
-
- 375 * 100% = 37.5%
-
Using Proportions:
- Setting up a proportion can be a useful technique, especially when dealing with more complex fractions.
- If you want to convert a fraction a/b to a percentage, you can set up the proportion:
- a/b = x/100
- Solve for x to find the percentage.
- Example: Convert 3/5 to a percentage.
- 3/5 = x/100
- Cross-multiply: 3 * 100 = 5 * x
- 300 = 5x
- x = 300 ÷ 5 = 60
- Therefore, 3/5 = 60%
-
Simplifying Complex Fractions:
- When dealing with complex fractions (fractions within fractions), simplify the fraction first before converting it to a percentage.
- Example: Convert (1/2) / (3/4) to a percentage.
- Simplify the complex fraction: (1/2) ÷ (3/4) = (1/2) * (4/3) = 4/6 = 2/3
- Convert 2/3 to a percentage: 2 ÷ 3 = 0.666...
-
- 666... * 100% ≈ 66.67%
-
Using Percentage Increase/Decrease Formulas:
- When calculating percentage increases or decreases, use the appropriate formulas:
- Percentage Increase = [(New Value - Original Value) / Original Value] * 100%
- Percentage Decrease = [(Original Value - New Value) / Original Value] * 100%
- When calculating percentage increases or decreases, use the appropriate formulas:
-
Estimation and Mental Math:
- Practice estimating percentages mentally. This is particularly useful in everyday situations where you need a quick approximation. For example, if you know that 1/8 is 12.5%, you can estimate that 3/8 is approximately 3 * 12.5% = 37.5%.
By mastering these advanced tips, you can enhance your skills in converting fractions to percentages and apply these techniques in various mathematical and real-world contexts.
Conclusion
In conclusion, understanding what percentage 1/8 represents is a fundamental skill with wide-ranging applications. As we have seen, 1/8 is equivalent to 12.5%. This conversion is not just a mathematical exercise but a practical tool that can be used in everyday situations such as calculating discounts, measuring ingredients, and interpreting statistical data.
By following the step-by-step guide provided, you can confidently convert 1/8 to 12.5%. Understanding the mathematical principles behind this conversion enhances your comprehension and ensures accuracy. Avoiding common mistakes and applying advanced tips further refines your skills, making you proficient in percentage conversions.
Whether you are a student, a professional, or simply someone who wants to improve their mathematical literacy, mastering the conversion of fractions to percentages is a valuable asset. The ability to quickly and accurately convert fractions like 1/8 to percentages empowers you to make informed decisions and understand the world around you more effectively.
Latest Posts
Latest Posts
-
50 Inches In How Many Feet
Dec 03, 2025
-
How Many Oz Is 2 Lbs
Dec 03, 2025
-
How Many Inches Is 45 Cm
Dec 03, 2025
-
How Many Minutes Are In 3 Hours
Dec 03, 2025
-
How Many Oz In 1 Liter
Dec 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.