What Is The Percent Of 3/2
bemquerermulher
Dec 03, 2025 · 9 min read
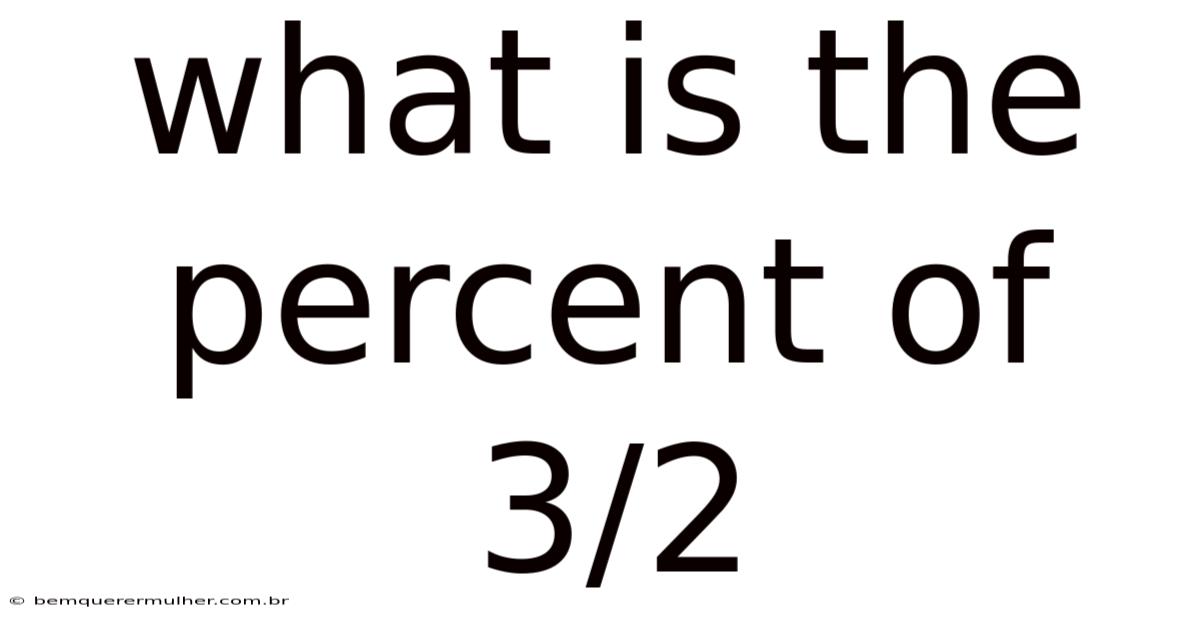
Table of Contents
Converting the fraction 3/2 to a percentage involves expressing it as a proportion out of 100. This conversion is fundamental in various fields, from finance to everyday problem-solving, allowing us to understand relative quantities more intuitively. The process is straightforward but essential for anyone looking to enhance their numerical literacy.
Understanding Percentages
Percentage means "per hundred" or "out of 100." A percentage is a way of expressing a ratio or fraction as a part of 100. For example, 50% means 50 out of 100, or simply one-half. Percentages are widely used because they provide a standardized way to compare different quantities, regardless of their original units or scales.
The Basics of Fractions
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). In the fraction 3/2:
- The numerator is 3.
- The denominator is 2.
This fraction indicates that we have three halves of something. A fraction where the numerator is greater than the denominator (like 3/2) is called an improper fraction. Improper fractions are greater than 1.
Converting Fractions to Decimals
Before converting a fraction to a percentage, it is often helpful to convert it to a decimal first. A decimal is another way of representing numbers that are not whole numbers. To convert a fraction to a decimal, you divide the numerator by the denominator.
Step-by-Step Conversion of 3/2 to a Percentage
Converting the fraction 3/2 into a percentage involves a few simple steps. By following these steps, anyone can easily convert fractions to percentages, enhancing their understanding and application of numerical concepts.
Step 1: Convert the Fraction to a Decimal
To convert the fraction 3/2 to a decimal, divide the numerator (3) by the denominator (2).
Calculation:
3 ÷ 2 = 1.5
So, the fraction 3/2 is equal to the decimal 1.5.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100. This is because a percentage represents a part out of 100.
Calculation:
1. 5 × 100 = 150
Therefore, the decimal 1.5 is equal to 150%.
Step 3: Add the Percent Sign
To finalize the conversion, add the percent sign (%) to the result. This indicates that the number is now expressed as a percentage.
Final Result:
150%
Thus, the fraction 3/2 is equivalent to 150%.
Alternative Method: Direct Conversion
Another method to convert a fraction to a percentage is to set up a proportion and solve for the percentage directly. This can be particularly useful when dealing with more complex fractions or when a calculator is not readily available.
Step 1: Set Up a Proportion
A proportion is an equation that states that two ratios are equal. In this case, we want to find what percentage (x) 3/2 represents. We can set up the proportion as follows:
3/2 = x/100
This equation states that the fraction 3/2 is equal to x percent out of 100.
Step 2: Solve for x
To solve for x, cross-multiply:
3 × 100 = 2 × x
300 = 2x
Now, divide both sides by 2 to isolate x:
300 / 2 = x
150 = x
Step 3: Add the Percent Sign
Add the percent sign to the value of x to express the result as a percentage.
Final Result:
150%
Using the direct proportion method, we also find that 3/2 is equal to 150%.
Real-World Applications
Understanding how to convert fractions to percentages is not just an academic exercise; it has numerous practical applications in everyday life.
Financial Analysis
In finance, percentages are used to express changes in stock prices, interest rates, and investment returns. For example, if an investment increases from $100 to $250, the percentage increase can be calculated as:
Increase = $250 - $100 = $150
Percentage Increase = (Increase / Original Amount) × 100
Percentage Increase = ($150 / $100) × 100 = 150%
This means the investment has increased by 150%.
Retail and Discounts
Retailers often use percentages to denote discounts and sales. For instance, a "30% off" sale means that the price is reduced by 30% of the original price. If an item originally costs $50, the discount amount is:
Discount Amount = (Percentage Discount / 100) × Original Price
Discount Amount = (30 / 100) × $50 = $15
The sale price would then be $50 - $15 = $35.
Cooking and Baking
In cooking and baking, recipes often require adjusting ingredient quantities. Percentages can help scale recipes up or down while maintaining the correct proportions. For example, if a recipe calls for 2 cups of flour and you want to increase the recipe by 50%, you would calculate:
Increase in Flour = (Percentage Increase / 100) × Original Amount
Increase in Flour = (50 / 100) × 2 cups = 1 cup
You would then add 1 cup of flour to the original 2 cups, resulting in a total of 3 cups of flour.
Academic Grading
Teachers use percentages to calculate and report student grades. If a student scores 45 out of 60 on a test, the percentage score is:
Percentage Score = (Score / Total Possible Score) × 100
Percentage Score = (45 / 60) × 100 = 75%
This means the student scored 75% on the test.
Common Mistakes to Avoid
While converting fractions to percentages is relatively straightforward, there are some common mistakes that people often make. Being aware of these pitfalls can help ensure accuracy in calculations.
Incorrect Division
One of the most common mistakes is dividing the denominator by the numerator instead of the numerator by the denominator when converting a fraction to a decimal. Always remember to divide the top number (numerator) by the bottom number (denominator).
Forgetting to Multiply by 100
After converting a fraction to a decimal, it is essential to multiply the decimal by 100 to express it as a percentage. Forgetting this step will result in an incorrect answer.
Misinterpreting the Percentage
Sometimes, people misinterpret what the percentage actually represents. Always ensure you understand the context and what the percentage is referring to. For example, a 150% increase means the new value is 2.5 times the original value, not just 1.5 times.
Rounding Errors
When dealing with decimals that have many digits, rounding errors can occur. It is best to keep as many decimal places as possible during the calculation and only round the final answer to the desired level of precision.
Advanced Concepts and Applications
Beyond basic conversions, percentages are used in more complex calculations and analyses.
Percentage Change
Percentage change is used to describe the relative difference between two values. The formula for percentage change is:
Percentage Change = ((New Value - Old Value) / Old Value) × 100
For example, if a company's revenue increases from $500,000 to $750,000, the percentage change is:
Percentage Change = (($750,000 - $500,000) / $500,000) × 100
Percentage Change = ($250,000 / $500,000) × 100 = 50%
This indicates a 50% increase in revenue.
Compound Interest
Compound interest is interest calculated on the initial principal, which also includes all of the accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
For example, if you invest $1,000 at an annual interest rate of 5% compounded annually for 10 years:
A = $1,000 (1 + 0.05/1)^(1*10)
A = $1,000 (1.05)^10
A ≈ $1,628.89
After 10 years, the investment would be worth approximately $1,628.89.
Statistical Analysis
In statistics, percentages are used to describe the distribution of data and to make inferences about populations. For example, if a survey finds that 60% of respondents prefer a certain product, this percentage can be used to estimate the proportion of the entire population that prefers the product.
Scientific Explanation
The conversion of fractions to percentages is rooted in mathematical principles that ensure consistency and accuracy in numerical representations. The concept leverages the base-10 decimal system, which is the foundation of modern arithmetic.
Decimal System
The decimal system is a base-10 number system, meaning it uses 10 digits (0-9) to represent numbers. Each position in a decimal number represents a power of 10. For example, in the number 123.45:
- 1 is in the hundreds place (10^2)
- 2 is in the tens place (10^1)
- 3 is in the ones place (10^0)
- 4 is in the tenths place (10^-1)
- 5 is in the hundredths place (10^-2)
Ratios and Proportions
A ratio is a comparison of two quantities, often expressed as a fraction. A proportion is an equation that states that two ratios are equal. Converting a fraction to a percentage involves expressing it as a proportion out of 100. This is based on the principle that percentages provide a standardized way to compare different quantities.
Mathematical Justification
The process of converting a fraction to a percentage can be mathematically justified as follows: Given a fraction a/b, we want to find the equivalent percentage x%. This can be expressed as:
a/b = x/100
To solve for x, we multiply both sides by 100:
x = (a/b) × 100
This formula ensures that the percentage x represents the same proportion as the original fraction a/b.
FAQ Section
Q: Why do we use percentages? A: Percentages provide a standardized way to compare different quantities, making it easier to understand relative values.
Q: Can a percentage be greater than 100%? A: Yes, a percentage can be greater than 100%. This indicates that the value is more than the original whole. For example, a 150% increase means the new value is 2.5 times the original value.
Q: How do I convert a mixed number to a percentage? A: First, convert the mixed number to an improper fraction. Then, convert the improper fraction to a decimal by dividing the numerator by the denominator. Finally, multiply the decimal by 100 and add the percent sign.
Q: What is the difference between percentage increase and percentage decrease? A: Percentage increase is used when a value increases, while percentage decrease is used when a value decreases. The formulas are:
- Percentage Increase = ((New Value - Old Value) / Old Value) × 100
- Percentage Decrease = ((Old Value - New Value) / Old Value) × 100
Q: How accurate are percentage calculations? A: The accuracy of percentage calculations depends on the precision of the initial values and the number of decimal places used during the calculation. To maintain accuracy, it is best to keep as many decimal places as possible until the final answer is rounded.
Conclusion
Converting the fraction 3/2 to a percentage is a fundamental mathematical skill with wide-ranging applications. Whether for financial analysis, retail discounts, cooking, or academic grading, understanding percentages enhances our ability to interpret and manipulate numerical data effectively. By following the step-by-step methods outlined in this article and avoiding common mistakes, anyone can confidently convert fractions to percentages and apply this knowledge in real-world scenarios. The scientific basis of this conversion, rooted in the decimal system and the principles of ratios and proportions, ensures that percentages remain a reliable and indispensable tool in quantitative analysis.
Latest Posts
Latest Posts
-
50 Inches In How Many Feet
Dec 03, 2025
-
How Many Oz Is 2 Lbs
Dec 03, 2025
-
How Many Inches Is 45 Cm
Dec 03, 2025
-
How Many Minutes Are In 3 Hours
Dec 03, 2025
-
How Many Oz In 1 Liter
Dec 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.