What Is A 23 Out Of 30
bemquerermulher
Dec 05, 2025 · 8 min read
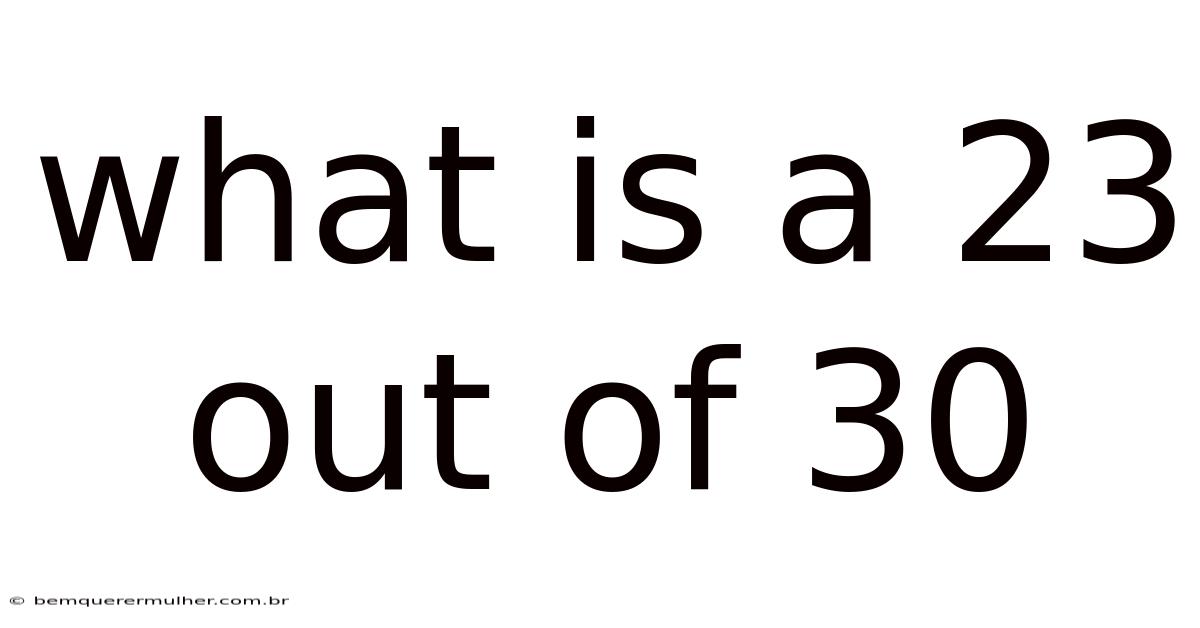
Table of Contents
Let's explore what "23 out of 30" means, how it is calculated, and how it applies in various real-world scenarios. Understanding fractions, percentages, and their applications can be very useful in many areas of life, from academic grading to everyday decision-making. This guide will provide you with a comprehensive explanation, examples, and practical tips to master this concept.
Understanding "23 Out of 30"
"23 out of 30" is a simple way to represent a fraction or a ratio. In this case, it means you have 23 parts out of a total of 30 parts. This kind of expression is commonly used to denote scores, proportions, or any situation where you need to show a part of a whole.
Basic Definition
At its core, "23 out of 30" is a fraction. A fraction is a way to represent a part of a whole. The number on top (23 in this case) is called the numerator, and it represents the number of parts you have. The number on the bottom (30 in this case) is called the denominator, and it represents the total number of parts.
How to Interpret
To interpret "23 out of 30," think of it as having a total of 30 possible units, and you possess or have achieved 23 of those units. For instance, if you took a quiz with 30 questions and answered 23 correctly, your score would be 23 out of 30.
Converting "23 Out of 30" to a Percentage
Converting fractions to percentages is a common task that helps in understanding the proportion in a more universally recognized format. Here's how you can convert "23 out of 30" to a percentage:
Step-by-Step Conversion
-
Divide the Numerator by the Denominator:
- Divide 23 by 30.
- 23 ÷ 30 = 0.766666...
-
Multiply by 100:
- Multiply the result by 100 to convert it to a percentage.
-
- 766666... × 100 = 76.6666...%
-
Round to the Desired Precision:
- Depending on how precise you need to be, you can round the percentage.
- For example, rounding to two decimal places gives you 76.67%.
- Rounding to one decimal place gives you 76.7%.
- Rounding to the nearest whole number gives you 77%.
Formula
The formula to convert any fraction to a percentage is:
Percentage = (Numerator ÷ Denominator) × 100
Example
Using the formula for "23 out of 30":
Percentage = (23 ÷ 30) × 100 = 76.67% (rounded to two decimal places)
Real-World Applications
Understanding what "23 out of 30" represents as a percentage is helpful in many real-world scenarios. Here are a few examples:
Academic Grading
In schools and universities, grades are often given as fractions. If a student scores 23 out of 30 on an exam, converting it to a percentage helps both the student and the teacher understand the performance relative to a standard 100% scale.
- Example: A student gets 23 out of 30 on a math test. This translates to approximately 76.67%, which might be a solid C+ or a B- depending on the grading scale.
Surveys and Statistics
Surveys often collect data that can be expressed as fractions. For example, if a survey of 30 people reveals that 23 prefer coffee over tea, this can be expressed as "23 out of 30." Converting this to a percentage provides a clearer picture of the preference.
- Example: In a survey, 23 out of 30 people prefer coffee. This means approximately 76.67% of the respondents prefer coffee.
Business and Sales
In business, understanding proportions and ratios is crucial. If a company closes 23 deals out of 30 attempted, this can be expressed as "23 out of 30." Converting it to a percentage helps in assessing the success rate.
- Example: A sales team closes 23 out of 30 deals. This means their success rate is approximately 76.67%.
Goal Setting and Progress Tracking
When setting goals, it's useful to track progress as a fraction. If you aim to read 30 books in a year and you've read 23, this can be expressed as "23 out of 30." Converting it to a percentage gives you a sense of how close you are to achieving your goal.
- Example: You've read 23 out of 30 books you aimed to read this year. This means you've completed approximately 76.67% of your reading goal.
Comparing "23 Out of 30" to Other Fractions
Comparing different fractions can provide additional context and understanding. Let's compare "23 out of 30" to some other common fractions:
Comparison with 3/4 (Three-Quarters)
- 3/4 as a Percentage: (3 ÷ 4) × 100 = 75%
- Comparison: "23 out of 30" (approximately 76.67%) is slightly higher than 3/4 (75%). This means that 23 out of 30 represents a slightly larger proportion than 3 out of 4.
Comparison with 2/3 (Two-Thirds)
- 2/3 as a Percentage: (2 ÷ 3) × 100 = 66.67%
- Comparison: "23 out of 30" (approximately 76.67%) is significantly higher than 2/3 (66.67%). This indicates that 23 out of 30 represents a much larger proportion than 2 out of 3.
Comparison with 4/5 (Four-Fifths)
- 4/5 as a Percentage: (4 ÷ 5) × 100 = 80%
- Comparison: "23 out of 30" (approximately 76.67%) is lower than 4/5 (80%). This means that 23 out of 30 represents a smaller proportion than 4 out of 5.
Summary Table
| Fraction | Percentage | Comparison to 23/30 |
|---|---|---|
| 3/4 | 75% | Slightly Higher |
| 2/3 | 66.67% | Significantly Higher |
| 4/5 | 80% | Lower |
Tips for Working with Fractions and Percentages
Working with fractions and percentages can become easier with practice. Here are some tips to help you master these concepts:
Practice Regularly
The more you work with fractions and percentages, the more comfortable you will become. Try solving different problems and applying these concepts in various real-life situations.
Use Online Calculators
There are many online calculators available that can help you convert fractions to percentages quickly. These tools can be useful for checking your work and saving time.
Understand the Basics
Make sure you have a solid understanding of the basic concepts of fractions, decimals, and percentages. This will make it easier to tackle more complex problems.
Break Down Complex Problems
If you encounter a complex problem involving fractions and percentages, try breaking it down into smaller, more manageable steps. This can make the problem less daunting and easier to solve.
Apply to Real Life
Look for opportunities to apply fractions and percentages in your daily life. This could be calculating discounts while shopping, figuring out proportions in cooking, or tracking your progress towards a goal.
Common Mistakes to Avoid
When working with fractions and percentages, it's easy to make mistakes. Here are some common pitfalls to watch out for:
Misunderstanding the Numerator and Denominator
Always remember that the numerator represents the number of parts you have, and the denominator represents the total number of parts. Mixing these up can lead to incorrect calculations.
Forgetting to Multiply by 100
When converting a fraction to a percentage, remember to multiply the result of the division by 100. Failing to do so will give you a decimal instead of a percentage.
Rounding Errors
Be careful when rounding percentages. Rounding too early or to the wrong number of decimal places can introduce errors into your calculations.
Incorrectly Comparing Fractions
When comparing fractions, make sure they have the same denominator or convert them to percentages for easier comparison. Comparing fractions with different denominators directly can be misleading.
Not Simplifying Fractions
Simplifying fractions before performing calculations can make the process easier. Always look for opportunities to simplify fractions to their lowest terms.
Advanced Applications
Beyond the basics, fractions and percentages are used in more advanced applications across various fields. Here are a few examples:
Finance
In finance, percentages are used to calculate interest rates, investment returns, and loan payments. Understanding how to work with percentages is crucial for making informed financial decisions.
- Example: Calculating the annual percentage yield (APY) on a savings account involves converting fractional interest rates to percentages.
Statistics
In statistics, percentages are used to represent probabilities, confidence intervals, and statistical significance. These concepts are essential for analyzing data and drawing meaningful conclusions.
- Example: Determining the confidence level of a survey result involves calculating percentages and understanding their implications.
Engineering
In engineering, percentages are used to calculate tolerances, error margins, and efficiency ratings. These calculations are critical for designing and building reliable systems.
- Example: Calculating the efficiency of a machine involves determining the percentage of input energy that is converted into useful output.
Data Analysis
In data analysis, percentages are used to summarize and present data in a clear and understandable format. This helps in identifying trends, patterns, and insights.
- Example: Analyzing customer demographics often involves calculating the percentage of customers in different age groups, income brackets, or geographic locations.
Conclusion
Understanding what "23 out of 30" means and how to convert it to a percentage is a valuable skill that can be applied in many areas of life. Whether you're a student tracking your grades, a business professional analyzing sales data, or simply someone trying to make sense of the world around you, mastering fractions and percentages will empower you to make more informed decisions. By following the steps, tips, and examples provided in this guide, you can confidently work with fractions and percentages and unlock their full potential. "23 out of 30" is just one example, but the principles you've learned can be applied to any fraction or ratio you encounter. Keep practicing, stay curious, and you'll find that working with numbers becomes second nature.
Latest Posts
Latest Posts
-
What Is 12 Out Of 20 As A Percent
Dec 05, 2025
-
What Percent Is 40 Of 60
Dec 05, 2025
-
What Is 37 2 Celsius In Fahrenheit
Dec 05, 2025
-
What Is The Molar Mass Of Co2
Dec 05, 2025
-
Fungi Number Of Cells Unicellular Or Multicellular
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about What Is A 23 Out Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.