39 Out Of 50 As A Percentage
bemquerermulher
Dec 06, 2025 · 7 min read
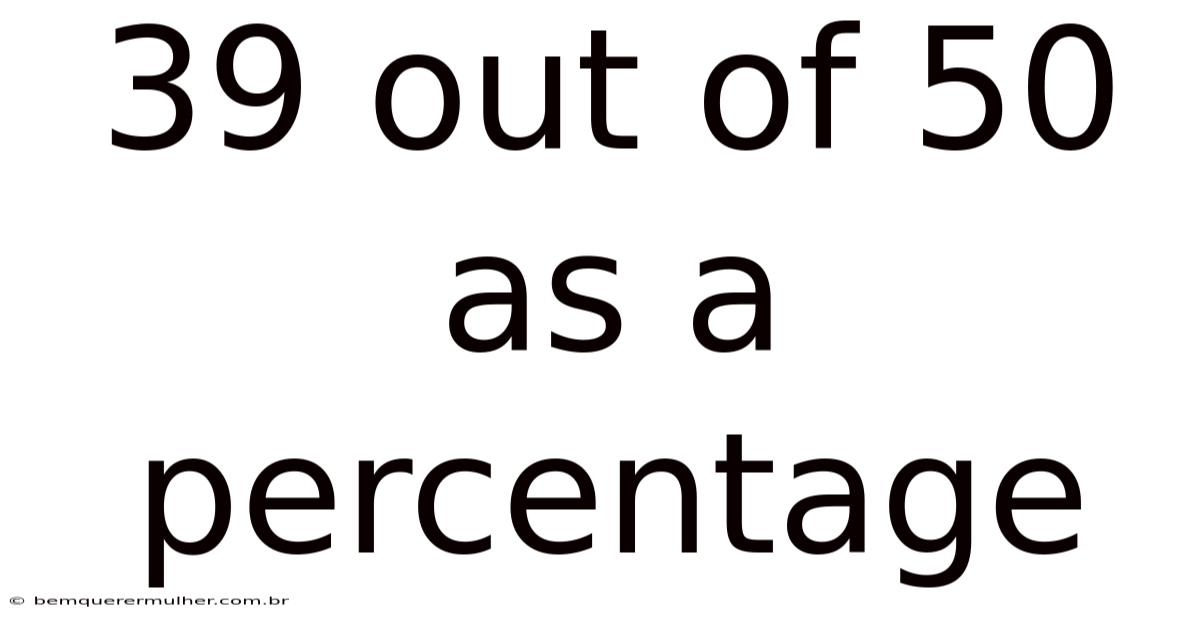
Table of Contents
Calculating percentages is a fundamental skill in mathematics with wide applications in everyday life, from figuring out discounts while shopping to understanding statistical data. Understanding how to convert a fraction, like 39 out of 50, into a percentage is particularly useful. This article will provide a comprehensive guide on how to calculate 39 out of 50 as a percentage, offering detailed explanations and practical examples to ensure clarity.
Introduction
Percentages are a standardized way of expressing fractions or ratios as a part of 100. They simplify comparisons and are used extensively in various fields, including finance, statistics, and education. Converting a fraction to a percentage helps in better understanding and interpreting the data. In this case, we want to determine what percentage 39 out of 50 represents. This calculation is straightforward but crucial for grasping more complex mathematical concepts.
Understanding the Basics: What is a Percentage?
Before diving into the calculation, it's important to understand what a percentage represents. The term "percent" comes from the Latin per centum, meaning "per hundred." A percentage is a ratio or fraction expressed as a part of 100. It's a dimensionless number, meaning it doesn't have any units of measurement.
Key Concepts
- Fraction: A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). In our case, 39 out of 50 is a fraction, where 39 is the numerator and 50 is the denominator.
- Ratio: A ratio compares two quantities. It can be expressed as a fraction.
- Percentage: A way of expressing a number as a fraction of 100. It's denoted by the symbol %.
Step-by-Step Guide: Converting 39 out of 50 to a Percentage
To convert 39 out of 50 to a percentage, follow these steps:
Step 1: Write the Fraction
The first step is to express the given information as a fraction. In this case, 39 out of 50 is written as:
39/50
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator by the denominator:
39 ÷ 50 = 0.78
This division results in the decimal 0.78.
Step 3: Convert the Decimal to a Percentage
To convert the decimal to a percentage, multiply the decimal by 100:
0.78 × 100 = 78
Add the percentage symbol (%) to the result:
78%
Therefore, 39 out of 50 as a percentage is 78%.
Alternative Method: Scaling the Denominator to 100
Another method to convert a fraction to a percentage is to scale the denominator to 100. This approach is useful when the denominator can be easily multiplied to reach 100.
Step 1: Identify the Scaling Factor
Determine what number you need to multiply the denominator (50) by to get 100. In this case:
50 × X = 100
Solving for X:
X = 100 ÷ 50 = 2
So, the scaling factor is 2.
Step 2: Multiply Both Numerator and Denominator by the Scaling Factor
Multiply both the numerator and the denominator by the scaling factor (2):
(39 × 2) / (50 × 2) = 78 / 100
Now, the fraction has a denominator of 100.
Step 3: Express as a Percentage
The numerator now directly represents the percentage:
78 / 100 = 78%
Thus, 39 out of 50 is 78%.
Practical Examples and Applications
Understanding how to calculate percentages is essential in various real-world scenarios. Here are some examples:
Example 1: Test Scores
Suppose a student scores 39 out of 50 on a test. To find the percentage score, you would calculate:
(39 / 50) × 100 = 78%
This means the student scored 78% on the test.
Example 2: Sales Discount
Imagine a store offers a discount where an item is 39% off its original price. If the original price is $50, the discount amount can be calculated as:
Discount = (39 / 100) × $50 = $19.50
The discounted price would be:
$50 - $19.50 = $30.50
Example 3: Survey Results
In a survey, 39 out of 50 people preferred a certain product. To express this as a percentage:
(39 / 50) × 100 = 78%
This means 78% of the people surveyed preferred the product.
Example 4: Budget Allocation
If a department allocates 39 out of 50 units of its budget to a specific project, the percentage allocation is:
(39 / 50) × 100 = 78%
So, 78% of the budget is allocated to the project.
Common Mistakes to Avoid
When calculating percentages, it's important to avoid common mistakes that can lead to incorrect results. Here are a few pitfalls to watch out for:
Mistake 1: Incorrect Division
Ensure you divide the numerator by the denominator correctly. A wrong division will lead to an inaccurate decimal and, consequently, an incorrect percentage.
Mistake 2: Forgetting to Multiply by 100
After obtaining the decimal, remember to multiply it by 100 to convert it to a percentage. Forgetting this step will give you a decimal answer instead of a percentage.
Mistake 3: Misunderstanding the Base
Always be clear about what the base (denominator) represents. For example, if you are calculating a percentage increase, ensure you use the original value as the base.
Mistake 4: Rounding Errors
When dealing with decimals that have many digits, rounding too early can affect the accuracy of the final percentage. Try to keep as many decimal places as possible until the final step.
The Importance of Understanding Percentages
Percentages are a fundamental tool for understanding and interpreting numerical data. They are used in a wide range of applications, including:
- Finance: Calculating interest rates, investment returns, and profit margins.
- Statistics: Analyzing data, conducting surveys, and interpreting results.
- Education: Grading tests, evaluating performance, and understanding statistics.
- Retail: Determining discounts, calculating sales tax, and understanding profit margins.
- Health: Interpreting medical data, understanding drug dosages, and analyzing health statistics.
Being proficient in calculating percentages enables you to make informed decisions, understand complex data, and communicate information effectively.
Advanced Concepts Related to Percentages
Once you've mastered the basic conversion of fractions to percentages, you can explore more advanced concepts:
Percentage Increase and Decrease
Percentage increase and decrease are used to describe the change in a quantity over time. The formulas are:
- Percentage Increase:
[(New Value - Original Value) / Original Value] × 100 - Percentage Decrease:
[(Original Value - New Value) / Original Value] × 100
Percentage Change
Percentage change is a general term that can refer to either percentage increase or decrease. It’s calculated using the formula:
[(New Value - Original Value) / Original Value] × 100
If the result is positive, it’s an increase; if it’s negative, it’s a decrease.
Weighted Averages
A weighted average is an average where some values contribute more than others. This is often used in calculating grades, where some assignments are worth more than others. The formula is:
Weighted Average = (W1 × V1 + W2 × V2 + ... + Wn × Vn) / (W1 + W2 + ... + Wn)
Where W represents the weight and V represents the value.
Compound Interest
Compound interest is interest calculated on the initial principal and also on the accumulated interest of previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Tools for Calculating Percentages
While calculating percentages manually is important for understanding the concept, several tools can help simplify the process:
Calculators
Basic calculators have percentage functions that allow you to quickly calculate percentages.
Online Percentage Calculators
Numerous websites offer percentage calculators. These tools often provide additional functionalities, such as calculating percentage increase, decrease, and differences.
Spreadsheet Software
Programs like Microsoft Excel and Google Sheets can be used to perform complex percentage calculations. They allow you to create formulas and automate calculations on large datasets.
Conclusion
Converting 39 out of 50 to a percentage is a straightforward process that involves dividing 39 by 50 and then multiplying by 100. The result, 78%, provides a clear understanding of the proportion. Mastering this basic calculation is essential for various applications in finance, statistics, and everyday life. By understanding the underlying concepts and practicing with different examples, you can confidently apply percentages in a wide range of scenarios. Whether you’re calculating test scores, discounts, or budget allocations, understanding percentages empowers you to make informed decisions and interpret data effectively.
Latest Posts
Latest Posts
-
Which Of These Phosphorylates Adp To Make Atp
Dec 06, 2025
-
How Much Is 15 Ounces In Cups
Dec 06, 2025
-
How Much Is 300 Ml In Oz
Dec 06, 2025
-
How Many Pints Are In 4 Gallons
Dec 06, 2025
-
In 10 Hours What Time Will It Be
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about 39 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.