3 And 3/8 As A Decimal
bemquerermulher
Dec 05, 2025 · 9 min read
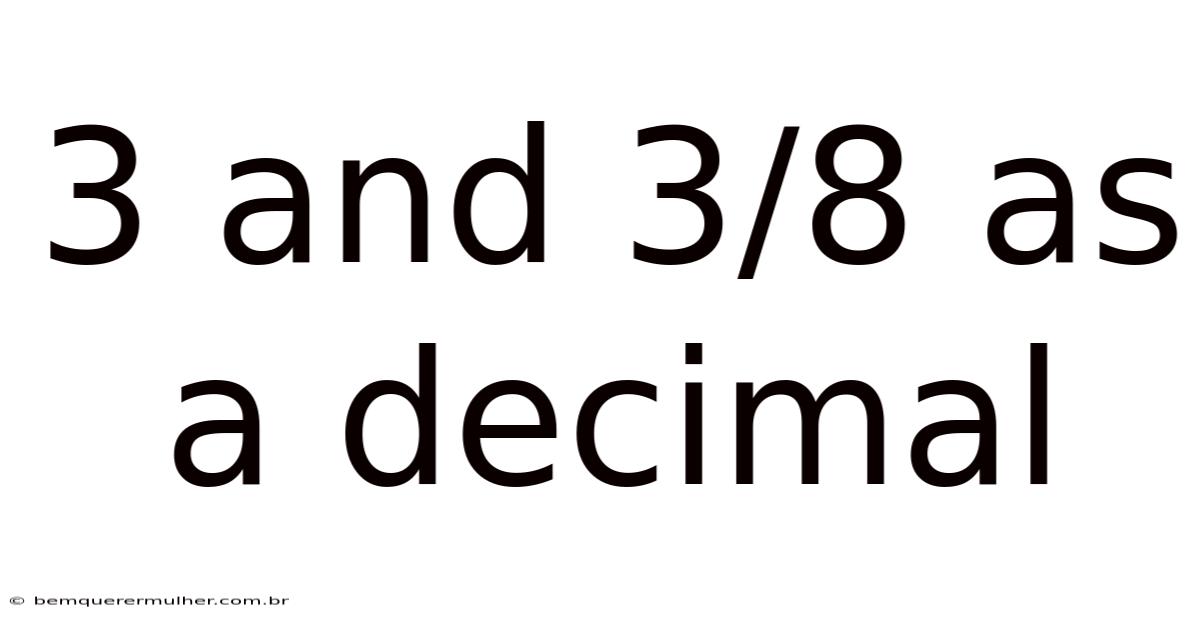
Table of Contents
Let's explore how to convert the mixed number 3 and 3/8 into a decimal. Understanding this conversion is useful in many areas, from cooking and crafting to engineering and finance. Converting fractions to decimals allows for more precise calculations and comparisons, making complex tasks simpler. This article will provide a step-by-step guide, additional context, and practical examples to ensure you fully understand the process.
Introduction
Converting 3 and 3/8 to a decimal involves understanding the relationship between mixed numbers, fractions, and decimals. A mixed number is a combination of a whole number and a fraction, while a decimal is a way of representing numbers using a base-10 system. In this case, 3 and 3/8 consists of the whole number 3 and the fraction 3/8. To convert this mixed number to a decimal, we need to convert the fractional part (3/8) into its decimal equivalent and then add it to the whole number.
Understanding the Basics: Fractions, Decimals, and Mixed Numbers
Before diving into the conversion process, let's define some basic terms:
- Fraction: A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator.
- Decimal: A decimal is a way of representing numbers that uses a base-10 system. Decimal numbers include a decimal point, which separates the whole number part from the fractional part. For example, 3.75 is a decimal number where 3 is the whole number and .75 is the fractional part.
- Mixed Number: A mixed number is a combination of a whole number and a fraction. For example, 3 and 3/8 is a mixed number where 3 is the whole number and 3/8 is the fraction.
Understanding these basic concepts is crucial for effectively converting mixed numbers to decimals.
Step-by-Step Guide: Converting 3 and 3/8 to a Decimal
Here's a step-by-step guide on how to convert the mixed number 3 and 3/8 into a decimal:
Step 1: Separate the Whole Number and the Fraction
The first step is to separate the whole number and the fraction in the mixed number. In this case, the mixed number is 3 and 3/8. So, we separate the whole number 3 from the fraction 3/8.
Step 2: Convert the Fraction to a Decimal
To convert the fraction 3/8 to a decimal, you need to divide the numerator (3) by the denominator (8). You can do this using long division or a calculator.
Long Division Method:
- Set up the long division: Divide 3 by 8.
- Since 3 is less than 8, add a decimal point and a zero to the end of 3, making it 3.0.
- Divide 30 by 8. 8 goes into 30 three times (3 x 8 = 24). Write 3 above the 0 after the decimal point.
- Subtract 24 from 30, which leaves 6.
- Add another zero to the end of 6, making it 60.
- Divide 60 by 8. 8 goes into 60 seven times (7 x 8 = 56). Write 7 after the 3 in the quotient.
- Subtract 56 from 60, which leaves 4.
- Add another zero to the end of 4, making it 40.
- Divide 40 by 8. 8 goes into 40 five times (5 x 8 = 40). Write 5 after the 7 in the quotient.
- Subtract 40 from 40, which leaves 0.
So, 3 ÷ 8 = 0.375.
Calculator Method:
Simply divide 3 by 8 using a calculator:
3 ÷ 8 = 0.375
Step 3: Add the Decimal to the Whole Number
Now that you have converted the fraction 3/8 to the decimal 0.375, you need to add this decimal to the whole number 3.
3 + 0.375 = 3.375
Therefore, 3 and 3/8 as a decimal is 3.375.
Understanding the Decimal Value of Common Fractions
To better understand the conversion of fractions to decimals, it's helpful to memorize the decimal values of some common fractions:
- 1/4 = 0.25
- 1/2 = 0.5
- 3/4 = 0.75
- 1/8 = 0.125
- 3/8 = 0.375
- 5/8 = 0.625
- 7/8 = 0.875
Recognizing these common fractions and their decimal equivalents can make conversions quicker and easier.
Practical Examples of Using Decimals
Decimals are widely used in various practical applications. Here are a few examples:
Cooking
In cooking, precise measurements are crucial for achieving the desired results. Recipes often call for ingredients in fractional amounts, such as 3/8 of a cup. Converting this fraction to a decimal (0.375 cup) allows for more accurate measurement using measuring cups or spoons with decimal markings.
Construction
In construction, measurements need to be extremely precise. When cutting materials like wood or metal, measurements are often given in decimals. For example, a piece of wood might need to be cut to 3.375 inches. Using a decimal representation ensures accuracy and reduces the risk of errors.
Finance
In finance, decimals are used extensively to represent monetary values. For instance, interest rates, stock prices, and currency exchange rates are all expressed as decimals. Understanding how to work with decimals is essential for making informed financial decisions.
Engineering
Engineering relies heavily on precise calculations. Measurements in engineering projects are often expressed as decimals to achieve the required level of accuracy. For example, the diameter of a pipe might be specified as 3.375 inches.
Converting Other Mixed Numbers to Decimals
The process for converting other mixed numbers to decimals is the same as the one described above. Here are a few more examples:
Example 1: Convert 5 and 1/4 to a Decimal
- Separate the whole number and the fraction: 5 and 1/4.
- Convert the fraction 1/4 to a decimal: 1 ÷ 4 = 0.25.
- Add the decimal to the whole number: 5 + 0.25 = 5.25.
So, 5 and 1/4 as a decimal is 5.25.
Example 2: Convert 2 and 5/8 to a Decimal
- Separate the whole number and the fraction: 2 and 5/8.
- Convert the fraction 5/8 to a decimal: 5 ÷ 8 = 0.625.
- Add the decimal to the whole number: 2 + 0.625 = 2.625.
So, 2 and 5/8 as a decimal is 2.625.
Example 3: Convert 7 and 7/8 to a Decimal
- Separate the whole number and the fraction: 7 and 7/8.
- Convert the fraction 7/8 to a decimal: 7 ÷ 8 = 0.875.
- Add the decimal to the whole number: 7 + 0.875 = 7.875.
So, 7 and 7/8 as a decimal is 7.875.
Common Mistakes to Avoid
When converting mixed numbers to decimals, there are a few common mistakes that you should avoid:
Mistake 1: Forgetting to Add the Whole Number
One of the most common mistakes is converting the fraction to a decimal but forgetting to add the whole number back in. Remember that the mixed number consists of both a whole number and a fraction, so you need to include both in your final answer.
Mistake 2: Incorrectly Dividing the Fraction
Another common mistake is dividing the fraction incorrectly. Make sure you are dividing the numerator by the denominator, not the other way around. Double-check your division to ensure you get the correct decimal value.
Mistake 3: Rounding Too Early
Rounding too early in the process can lead to inaccuracies in your final answer. If you need to round the decimal, wait until the very end of the calculation to do so.
Mistake 4: Misunderstanding Place Value
Understanding place value is crucial when working with decimals. Make sure you understand the value of each digit after the decimal point (tenths, hundredths, thousandths, etc.) to avoid errors in your calculations.
Advanced Tips and Tricks
Here are some advanced tips and tricks to help you become even more proficient at converting mixed numbers to decimals:
Tip 1: Use Benchmarks
Using benchmarks can help you quickly estimate the decimal value of a fraction. For example, you know that 1/2 is 0.5, so any fraction slightly less than 1/2 will be slightly less than 0.5.
Tip 2: Simplify Fractions First
If the fraction can be simplified, doing so before converting it to a decimal can make the division easier. For example, if you have the fraction 4/8, you can simplify it to 1/2 before converting it to 0.5.
Tip 3: Practice Regularly
The more you practice converting mixed numbers to decimals, the more comfortable and confident you will become. Try working through a variety of examples to reinforce your understanding.
Tip 4: Use Online Resources
There are many online resources available to help you practice and improve your skills. Websites and apps that offer fraction-to-decimal converters can be valuable tools for checking your work and learning new strategies.
The Importance of Precision in Conversions
Precision is critical when converting fractions to decimals, especially in fields like engineering, finance, and science. Even small errors can lead to significant discrepancies and potentially costly mistakes. For example, in engineering, an imprecise measurement could result in a structural flaw. In finance, it could lead to incorrect calculations of interest or investment returns.
To ensure precision, always double-check your work and use reliable tools, such as calculators or conversion charts. If you are performing calculations manually, take your time and pay close attention to each step.
Real-World Applications
Converting mixed numbers to decimals is not just an academic exercise; it has numerous real-world applications. Here are a few more examples:
Carpentry
Carpenters often need to work with measurements that are given in mixed numbers, such as 3 and 3/8 inches. Converting these measurements to decimals allows them to use precision measuring tools and ensure accurate cuts.
Sewing
In sewing, fabric measurements are often given in fractions. Converting these fractions to decimals can help seamstresses create garments with precise dimensions.
Pharmaceuticals
In the pharmaceutical industry, precise measurements are essential for compounding medications. Pharmacists often need to convert fractions to decimals to ensure the correct dosage of each ingredient.
Surveying
Surveyors use decimals to represent distances and elevations. Converting mixed numbers to decimals allows them to create accurate maps and plans.
Conclusion
Converting the mixed number 3 and 3/8 to a decimal is a straightforward process that involves separating the whole number and fraction, converting the fraction to a decimal, and then adding the two together. The result, 3.375, is a decimal representation that is commonly used in various fields requiring precision and accuracy. By understanding the basic concepts and following the step-by-step guide, you can confidently convert any mixed number to a decimal. With practice, you'll find this skill becomes second nature, enabling you to tackle mathematical problems with greater ease and accuracy in both academic and real-world settings. Remember to avoid common mistakes, use advanced tips, and appreciate the importance of precision in your conversions to excel in this area.
Latest Posts
Latest Posts
-
16 Feet Is How Many Inches
Dec 05, 2025
-
How Many Liters To A Gallon
Dec 05, 2025
-
How Many Feet Is In 30 Meters
Dec 05, 2025
-
3 And 3 8 As A Decimal
Dec 05, 2025
-
40 Inches Is How Many Feet
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about 3 And 3/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.